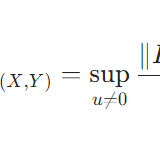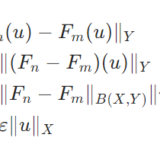有界線形作用素のなす空間B(X,Y)がノルム空間となることの証明

どうも、木村（@kimu3_slime）です。

今回は、有界線形作用素のなす空間\(B(X,Y)\)がノルム空間となることの証明を紹介します。

導入
証明
こちらもおすすめ

導入

\(X,Y\)をノルム空間とし、有界線形作用素のなす線形空間を\(B(X,Y)\)としましょう。

作用素ノルムとは、

\[\|F\|_{B(X,Y)}:= \inf \{M \mid \\すべてのu\in Xに対し \|F(u)\|_{Y} \leq M\|u\|_{X}\}\]

\[\|F\|_{B(X,Y)}= \sup_{u \neq 0} \frac{\|F(u)\|_{Y}}{\|u\|_{X}} = \sup _{\|u\|_{X} =1} \|F(u)\|_Y\]

のことです。これらの定義は、論理的に同値です。

この作用素ノルムが抽象ノルムの定義を満たすこと、\(B(X,Y)\)がノルム空間となることを証明しましょう。

証明

\(V\)を線形空間とする。1変数関数\(\| \cdot \| :V \to \mathbb{R}\)は、次を満たすときノルムと呼ばれる。

任意の\(a,b\in V\)、\(\lambda \in \mathbb{R}\)に対し、

(1) 正定値性：\(\|a\| \geq 0\)。\(a= 0\)は\(\|a\| = 0\)と同値である。

(2) 斉次性：\(\|\lambda a\| = |\lambda| \| a\| \)

(3) 三角不等式（劣加法性）：\(\|a+b\| \leq \|a\|+ \|b\|\)

ノルムを持つ線形空間を、ノルム空間と呼ぶ。

これらの条件を、\(\|F\|_{B(X,Y)}= \sup_{u \neq 0} \frac{\|F(u)\|_{Y}}{\|u\|_{X}}\)について確かめましょう。

正定値性について。

\(u \neq 0\)とすると、\(X,Y\)のノルムの正定値性から、\(\frac{\|F(u)\|_{Y}}{\|u\|_{X}} \geq 0\)です。したがって、上限を取れば、上限は上界なので、\(\|F\|_{B(X,Y)}= \sup_{u \neq 0} \frac{\|F(u)\|_{Y}}{\|u\|_{X}} \geq \frac{\|F(u)\|_{Y}}{\|u\|_{X}} \geq 0\)です。

また、作用素として0になることは、ゼロ作用素\(F=O\)であることを意味します。ゼロ作用素については、\(u \neq 0\)に対し、\(Y\)のノルムの正定値性から、\(\frac{\|O(u)\|_{Y}}{\|u\|_{X}} = \frac{\|0\|_Y}{\|u\|_X}= 0\)です。したがって0は上界で、上限は最小の上界なので、 \(\sup_{u \neq 0} \frac{\|F(u)\|_{Y}}{\|u\|_{X}} \leq 0\)です。さきほど示した\(\|F\|_{B(X,Y)} \geq 0\)と合わせれば、\(\|F\|_{B(X,Y)}=0\)となります。

逆に、\(\|F\|_{B(X,Y)}=0\)と仮定しましょう。0は上界なので、すべての\(u \neq 0\)に対し、\(\frac{\|F(u)\|_{Y}}{\|u\|_{X}} \leq 0\)です。左辺は\(X,Y\)のノルムの正定値より非負なので、\(\|F(u)\|_Y =0\)となります。再び\(Y\)のノルムの正定値性から、\(F(u)=0\)です。\(u=0\)のときは、\(F\)の線形性から、\(F(0)=0\)です。以上により、すべての\(u \in X\)に対し、\(F(u)=0\)なので、それはゼロ作用素\(F=O\)となることが示せました。

斉次性について。

上限の一般的な性質として、\(A \subset \mathbb{R}\)、\(\lambda A :=\{\lambda a \in a \in A\}\)とするとき、\(\sup (\lambda A) =\lambda \sup A\)となります。

上限の数列による特徴づけを用いて示しましょう。\( A\)の点列\((a_n)\)で、\(\lim_{n\to \infty} a_n = \sup A\)を満たすものが存在します。収束する数列の定数倍は収束し、極限の線形性より\(\lim_{n\to \infty} \lambda a_n = \lambda (\lim_{n\to \infty}a_n)= \lambda \sup A\)です。つまり、\(b_n:= \lambda a_n\)は\(\lambda A\)の点列で、\(\lambda \sup A\)に収束します。また、すべての\(a\)に対し\(\lambda a \leq \lambda \sup A\)なので、\(\lambda \sup A\)は\(\lambda A\)の上界です。よって、再び上限の数列による特徴づけにより、\(\sup (\lambda A) =\lambda \sup A\)が示せました。

そして、\(Y\)のノルムの斉次性を用いれば、

\[\begin{aligned} &\|\lambda F\|_{B(X,Y)} \\ &= \sup_{u \neq 0} \frac{\|\lambda F(u)\|_{Y}}{\|u\|_{X}} \\&= \sup_{u \neq 0} |\lambda| \frac{\|F(u)\|_{Y}}{\|u\|_{X}} \\ &= |\lambda| \sup_{u \neq 0} \frac{\|F(u)\|_{Y}}{\|u\|_{X}}\\ &= |\lambda| \| F\|_{B(X,Y)}\end{aligned}\]

が示せました。

三角不等式について。

\(F,G \in B(X,Y)\)とし、\( u \neq 0 \)について、\(Y\)のノルムの三角不等式から

\[\begin{aligned} &\frac{\|(F+G)(u)\|_{Y}}{\|u\|_{X}} \\ &= \frac{\|F(u)+G(u)\|_{Y}}{\|u\|_{X}} \\ & \leq \frac{\|F(u)\|_Y+\|G(u)\|_Y}{\|u\|_X} \\&\leq \|F\|_{B(X,Y)}+ \|G\|_{B(X,Y)}\end{aligned}\]

となります。したがって、上限は最小の上界なので、

\[\begin{aligned} & \|F+G\|_{B(X,Y)}\\ &= \sup_{u \neq 0} \frac{\|(F+G)(u)\|_{Y}}{\|u\|_{X}} \\ &\leq \|F\|_{B(X,Y)}+ \|G\|_{B(X,Y)} \end{aligned}\]

が示せました。

以上、有界線形作用素のなす空間\(B(X,Y)\)がノルム空間となることの証明を紹介してきました。

さらにこのノルムについて\(B(X,Y)\)は完備である：バナッハ空間となります。これについては別記事で。

木村すらいむ（@kimu3_slime）でした。ではでは。