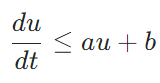常微分方程式の比較定理とは、証明

どうも、木村（@kimu3_slime）です。

今回は、常微分方程式の比較定理とは、その証明について紹介します。

常微分方程式の比較定理
例、劣解・優解
証明
こちらもおすすめ

常微分方程式の比較定理

常微分方程式の比較定理（comparison theorem）

\(T>0\)とし、関数\(u,v : [0,T]\to \mathbb{R}\)がそれぞれ

\[\frac{du}{dt} \leq f(u,t)\]

\[\frac{dv}{dt} = f(v,t)\]

\[u(0) \leq v(0)\]

を満たすとしましょう。\(f(s,t)\)は\(s\)について\(t\)によらず局所リプシッツ連続、かつ\(t\)について連続とします（このとき、微分方程式を満たす\(v\)は一意に存在します）。

このとき、\([0,T]\)上で\(u(t) \leq v(t)\)が成り立つ。

仮定の不等号の向きを逆にすると、

\[\frac{dw}{dt} \geq f(w,t)\]

\[w(0) \geq v(0)\]

結論も逆向きの不等号で成り立つ\(w(t) \geq v(t)\)。

例、劣解・優解

証明に進む前に、簡単な具体例を通じて正しそうか考えてみましょう。

\[\frac{dv}{dt} = 3v\]

という方程式を考えます（\(f(s,t)=3s\)）。その解は\(v(t) = v_0 e^{3t}\)です。

\(u\)として\(u(t)= u_0 e^{t}\)を考えると、\(u _0 \geq 0\)のとき、\(\frac{du}{dt} = u \leq 3u \)を満たします。例えば\(u_0 =v_0 =1\)のとき、比較定理の前提を満たします。そして実際、\(u(t) = e^{t} \leq e^{3t}\)は常に成り立ちますね。

画像引用：WolframAlpha e^t, e^{3t}

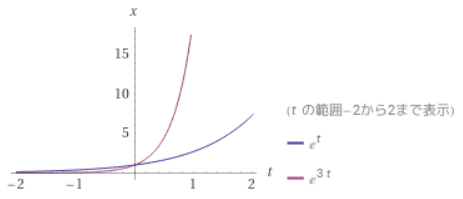
方程式と初期条件に大小関係があれば、それがその後も保たれ続けるというのが比較定理です。

\(u\)の増加率は、\(v\)の増加率に比べると常に同じか小さいので、差が覆らないのは妥当な結論に見えます。

微分方程式

\[\frac{dv}{dt} = f(v,t)\]

に対し、微分不等式

\[\frac{du}{dt} \leq f(u,t)\]

の解\(u\)を、劣解（subsolution）と呼びます。逆に、

\[\frac{dw}{dt} \geq f(w,t)\]

の解\(w\)を優解（supersolution）と呼びます。

微分方程式の解、劣解、優解について、\(u(0)\leq v(0) \leq w(0)\)ならば、常に\(u(t) \leq v(t) \leq w(t)\)が成り立つわけです。

証明

では、比較定理を証明していきましょう。次の方針で示します。

\(u(t) \leq v_n(t)\)となるような解の列\((v_n)\)を構成する
\((v_n)\)が収束する部分列を持ち、その極限\(v^{*}\)が微分方程式の解となることを示す
解の一意性より\(v^{*}=v\)で、\(u(t) \leq v(t)\)が言える

近似列の構成

まず、微分方程式を近似する方程式として、

\[\frac{dv_n}{dt} = f(v_n,t)+\frac{1}{n} \\ v_n(0)=v(0)\]

の解\(v_n\)を考えましょう。

すべての\(n\)に対し、\([0,T]\)上で\(u(t) \leq v_n(t)\)であることを、背理法によって示します。

仮に\(u(t_1) > v_n(t_1)\)である\(t_1 \in (0,T)\)、\(n\)が存在したとしましょう。

すると、\(u(t)=v(t)\)を満たす\(t\)の中で、最大のものとして\(t_2 \in (0,t_1)\)が存在します。\(u(t_2)=v_n(t_2)\)であって、\(t \in (t_2,t_1)\)ならば\(u(t) > v(t)\)です。そこで\(t_2\)における微分係数を考えると、

\[\frac{u(t_2 +h)-u(t_2)}{h}> \frac{v_n(t_2+h)-v_n(t_n)}{h} \]

です。\(h\to 0\)の極限を取れば、不等式は保たれるので、

\[\begin{aligned} & \frac{du}{dt}(t_2)\\ &\geq \frac{dv_n}{dt}(t_2) \\&= f(v_n(t_2),t_2)+\frac{1}{n} \\ &= f(u(t_2),t_2)+\frac{1}{n} \\ &>f(u(t_2),t_2)\end{aligned}\]

です。これは仮定\(\frac{du}{dt} \leq f(u,t)\)に矛盾します。

よって、すべての\(n\)に対し、\([0,T]\)上で\(u(t) \leq v_n(t)\)です。

近似列の収束

こうしてできた関数列\((v_n)\)は、収束する部分列を持ちます。

アルツェラ・アスコリの定理を用いましょう。

アルツェラ・アスコリの定理（Arzelà–Ascoli theorem）

\(K \subset \mathbb{R}^N\)をコンパクト集合、\((f_n)\)を\(K\)上の連続関数列とする。

一様に有界：「すべての\(n\)に対し、\(\sup_{x \in K}\|f_n(x)\| \leq M\)」を満たす\(M\)が存在する
同程度に連続：すべての\(n\)、\(\varepsilon>0\)に対し、「\(x,y\in K\)が\(\|x-y\|\leq \delta\)ならば\(\|f_n(x)-f_n(y)\| \leq \varepsilon\)」を満たす\(\delta >0\)が存在する

ならば、\((f_n)\)は\(K\)上で一様収束する部分列を持つ。

特に、\(K=[a,b]\)、\((f_n)\)が一様有界かつ微分可能で、導関数\((f_n^{\prime})\)も一様有界ならば、定理の仮定を満たす。

まず、\((v_n)\)は微分方程式の解として\(C^1\)級です。

\(f(s,t)\)の連続性から、\([v_0-1,v_0+1]\times[0,T]\)において最大値\(M\)を持つため、\(|f(s,t)| \leq M\)としましょう。解の連続性より、\([0,t_3]\)上で\(v_n (t) \in [v_0-1,v_0+1]\)となるような\(t_3 \leq T\)が存在します。

微分方程式を積分すると、三角不等式より

\[\begin{aligned} &|v_n(t)| \\ &= |v_n(0)+\int_{0}^t (f(v_n,s)+\frac{1}{n})ds| \\& \leq |v(0)| + \int_{0}^T | M+1|ds\\ &\leq |v(0)| + T| M+1| \end{aligned}\]

となるので、\((v_n)\)は\([0,T]\)上で一様に有界です。また、\(f(s,t)\)は\(s\)について\(t\)によらず局所リプシッツ連続なので

\[\begin{aligned} &|\frac{dv_n}{dt}(t)| \\ &= |f(v_n(t),t)+\frac{1}{n}| \\& \leq L|v_n(t)|+1 \end{aligned}\]

となり、\((v_n)\)が一様に有界であることから、\((\frac{dv_n}{dt})\)も一様に有界です。

したがって、アルツェラ・アスコリの定理より、\((v_n)\)は一様収束する部分列\((v_{n_j})\)を持ちます。その極限を\(v^{*}\)としましょう。

一様収束しているならば、極限の順序交換、\(n\)の極限と微分の極限の順序交換が可能です。

\[\begin{aligned} & \frac{dv^{*}}{dt}(t) \\ &= \lim_{j\to \infty} \frac{dv_{n_j}}{dt}(t) \\&= \lim_{j\to \infty}(f(v_{n_j},t)+ \frac{1}{n_j}) \\&= f(v^{*},t)\end{aligned}\]

となるので、\(v^{*}\)は微分方程式\(\frac{dv}{dt} = f(v,t)\)の解です。