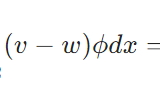どうも、木村(@kimu3_slime)です。
今回は、ローレンツ方程式のアトラクターの存在証明を紹介します。
3次元空間\(\mathbb{R}^3\)におけるローレンツ方程式
\[\left\{ \begin{array}{l} \frac{dx}{dt} = -\sigma x +\sigma y \\ \frac{dy}{dt} = rx -y-xz \\ \frac{dz}{dt} = xy – bz \end{array} \right.\]
を考えましょう。パラメータは\(\sigma,r,b > 0\)です。
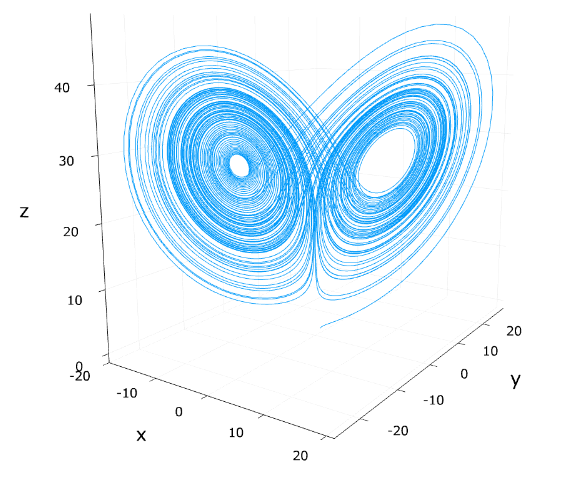
ローレンツ方程式にグローバルアトラクターが存在することをしましましょう。
グローバルアトラクターの構成方法として、コンパクト吸収集合\(B\)の存在を示せば十分です。
\(B\)が吸収集合であることの十分条件は、すべての初期値\((x_0,y_0,z_0)\)に対し、「すべての\(t\)に対し\(t \geq T\)ならば\((x(t),y(t),z(t)) \in B\)」を満たす\(T>0\)が存在することです。
今回は、大きな球\(B :=\{(x,y,z) \mid x^2+y^2 +(z-r-\sigma)^2 \leq R^2\}\)が吸収集合であることを示しましょう。\(R\)は後で具体的に指定します。
そこで解の大きさを評価する\(V(x,y,z):=x^2+y^2 +(z-r-\sigma)^2\)という関数を考えます。
解\((x(t),y(t),z(t))\)との合成を考えると、時間微分\(\frac{dV}{dt}(x(t),y(t),z(t))\)を計算できます。その微分を不等式評価して、グロンウォールの不等式に持ち込みましょう。
グロンウォールの不等式(Gronwall’s inequality)
\(T>0 \)、\(a,b\in \mathbb{R}\)、\(u:[0,T]\to \mathbb{R}\)とする。\(u\)が微分不等式
\[\frac{du}{dt _{+}} \leq au+b\]
を満たすならば、
\[u(t) \leq (u_0 +\frac{b}{a})e^{at}-\frac{b}{a}\]
が成り立つ。\(\frac{du}{dt _{+}}\)は\(u\)の右側微分係数。
もし\(a\)が負ならば、指数関数的減衰によって\(u\)は有界と言えるわけですね。証明はRobinson「Infinite-Dimensional Dynamical Systems」などを参照してください。
\(V=x^2+y^2 +(z-r-\sigma)^2\)を解に沿って時間微分すれば、合成関数の微分(チェインルール)より、
\[\begin{aligned} & \frac{dV}{dt}(x(t),y(t),z(t))\\ &= \frac{\partial V}{\partial x}\frac{dx}{dt} + \frac{\partial V}{\partial y}\frac{dy}{dt} + \frac{\partial V}{\partial z}\frac{dz}{dt} \\ &= 2x(-\sigma x +\sigma y)+2y(rx -y-xz)\\&\quad +2(z-r-\sigma)(xy – bz)\\ &= -2\sigma x^2 -2y^2 -2bz^2+2b(r+\sigma) z \\&= -2\sigma x^2 -2y^2 -b(z-r-\sigma)^2\\&\quad-bz^2+b(r+\sigma)^2\\& \leq -2\sigma x^2 -2y^2 -b(z-r-\sigma)^2+b(r+\sigma)^2\end{aligned}\]
ここで係数を共通化させるために、\(\alpha := \min \{2\sigma ,2,b\}\)と置けば、\(\alpha >0\)で、
\[\begin{aligned} & \frac{dV}{dt}\\ &\leq -\alpha (x^2 +y^2 +(z-r-\sigma)^2)+b(r+\sigma)^2 \\ &= -\alpha V +b(r+\sigma)^2\end{aligned}\]
となりました。これがグロンウォールの不等式の適用できる形で、
\[V(x(t),y(t),z(t)) \\ \leq (V_0 -\frac{b(r+\sigma)^2}{\alpha})e^{-\alpha t}+\frac{b(r+\sigma)^2}{\alpha}\]
となります。\(\alpha>0\)なので、\(V_0=x_0^2+y_0^2+(z_0-r-\sigma)^2\)が何であっても、右辺の第一項は単調減少で、\(\lim_{t\to \infty} (V_0 -\frac{b(r+\sigma)^2}{\alpha})e^{-\alpha t}=0\)です。よって、「\(t\geq T\)ならば
\[V(x(t),y(t),z(t)) \\ \leq \frac{2b(r+\sigma)^2}{\alpha}\]
」を満たすような\(T\)が存在します。
以上の結果をもとに、半径\(R\)を\(R^2 = \frac{2b(r+\sigma)^2}{\alpha}\)を満たす数とし、\(B :=\{(x,y,z) \mid x^2+y^2 +(z-r-\sigma)^2 \leq R^2\}\)を考えましょう。どんな初期値\((x_0,y_0,z_0)\)に対しても、「\(t\geq T\)ならば
\[(x(t))^2+(y(t))^2+ (z(t)-r-\sigma)^2 \\ =V(x(t),y(t),z(t)) \\ \leq \frac{2b(r+\sigma)^2}{\alpha}\]
」を満たすような\(T\)が存在します。つまり、\(t\geq T\)ならば\((x(t),y(t),z(t)) \in B\)です。よって、\(B\)は吸収集合です。ユークリッド空間の有界な閉集合でもあるので、コンパクトです。
以上によりコンパクトな吸収集合が存在すること、力学系が散逸的であることが示せたので、ω極限集合\(A:=\omega (B)\)がグローバルアトラクターとして存在することが示せました。
以上、ローレンツ方程式のアトラクターの存在証明を紹介してきました。
このアトラクターの形状について詳細な情報はこの証明からはわかりませんが、少なくとも解が大きな球に吸い込まれていくことがわかりますね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)