どうも、木村(@kimu3_slime)です。
今回は、グロンウォールの不等式とは、その証明を紹介します。
グロンウォールの不等式とは
グロンウォールの不等式(Gronwall’s inequality)、またはグロンウォールの補題(Gronwall’s lemma)とは、次のような主張です。
\(g,h\)を連続関数として、未知関数\(u\)が微分不等式
\[\frac{du}{dt} \leq g(t)u+h(t)\]
を満たすならば、
\[u(t) \leq u(0)e^{G(t)}+ \int_0^t e^{G(t)-G(s)}h(s)ds \]
\[G(t): = \int_0 ^t g(r)dr\]
を満たす。
特に、\(g(t)=a, h(t)=b\)という定数の場合、
\[\frac{du}{dt} \leq au+b\]
を満たすならば、
\[u(t) \leq (u(0)+\frac{a}{b})e^{at} – \frac{b}{a} \]
を満たす。
\(u(t)\)の右辺は複雑な形に見えるかもしれませんが、不等式の右辺を等号にした微分方程式\(\frac{dv}{dt}=g(t)u+h(t)\)の解\(v(t)\)です。グロンウォールの不等式といっても、これとは少し形が違う主張もありますが、本質的には同様の考え方でしょう。
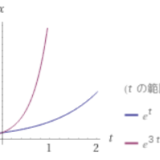
特に後半の主張はシンプルで使いやすいです。未知関数の時間微分\(\frac{du}{dt}\)を不等式評価して、係数\(a\)が負の1次関数で抑えられるならば、\(u\)は有界(\(e^{at}\)によって時間減衰するので)と言えます。これはローレンツ方程式のアトラクターの存在証明で応用されるものです。
証明
では証明していきましょう。常微分方程式の比較定理
\(T>0\)とし、関数\(u,v : [0,T]\to \mathbb{R}\)がそれぞれ
\[\frac{du}{dt} \leq f(u,t)\]
\[\frac{dv}{dt} = f(v,t)\]
\[u(0) \leq v(0)\]
を満たすとしましょう。\(f(s,t)\)は\(s\)について\(t\)によらず局所リプシッツ連続、かつ\(t\)について連続とします(このとき、微分方程式を満たす\(v\)は一意に存在します)。
このとき、\([0,T]\)上で\(u(t) \leq v(t)\)が成り立つ。
で、ほぼ結論が出ています。
\(f(s,t):=g(t)s+h(t)\)、\(\frac{dv}{dt}=g(t)u+h(t)\)、\(v(0)=u(0)\)として、比較定理を用いましょう。
\(\frac{dv}{dt}=g(t)u+h(t)\)は1階線形微分方程式であり、解き方が知られています。
\[G(t): = \int_0 ^t g(r)dr\]
が積分因子であり、これを方程式の両辺にかけて整理すれば、
\[v(t) = u(0)e^{G(t)}+ \int_0^t e^{G(t)-G(s)}h(s)ds\]
が導けます。比較定理より、\(u(t) \leq v(t)\)なので、結論が示せました。
後半\(g(t)=a,h(t)=b\)は、特殊ケースです。確かめてみましょう。
積分因子は\(G(t) = \int_0^t a dr =at\)です。したがって、
\[\begin{aligned} &v(t) \\ &=u(0)e^{at}+\int_0^t e^{at-as}b ds \\ &= u(0)e^{at}+[-\frac{b}{a}e^{at-as}]_{s=0}^{s=t}\\ &= (u(0)+\frac{a}{b})e^{at} – \frac{b}{a} \end{aligned}\]
と導くことができました。
以上、グロンウォールの不等式とは、その証明を紹介してきました。
グロンウォールの不等式からは、初期条件に関する連続依存性を導くこともできます。
未知の関数を既知の関数と不等式によって比較すると、未知の関数であっても引き出せる情報は増えます。複雑な方程式を解かずにその解の情報を得る方法のひとつとして、不等式比較を知っておくと良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)