一点と集合の距離、集合間の距離とは：ユークリッド空間を例に

どうも、木村（@kimu3_slime）です。

今回は、一点と集合の距離、集合間の距離とは何か、ユークリッド空間を例に紹介します。

導入と定義
1点と集合の距離：1次元
集合間の距離：1次元
集合間の距離：2次元の例
こちらもおすすめ

導入と定義

力学系\(H,((S(t)))\)のアトラクター\(A\)の定義として要請する性質として、それが他の有界な解集合\(K\)を引き寄せる

\[\lim_{t \to \infty} d(S(t)K, A ) =0\]

というものがあります。「引き寄せ具合」を定義するには、集合と集合の間の距離\(d(A,B)\)を何らかの形で定義する必要があるわけです。

では定義していきましょう。\((X,d)\)を距離空間、\(A,B \subset X\)を有界な部分集合とします。

1点と集合の間の距離は、\(a \in A\)に対し、

\[d(a,B) : = \inf_{b\in B}d(a,b)\]

と下限\(\inf\)で定義します。いわば、\(a\)との距離を最も小さくするような\(B\)の要素を（これ以上小さくできないよう）「選んだ」ときの距離です。

集合\(A,B\)間の距離は、

\[d(A,B) : = \sup _{a \in A}\inf_{b\in B}d(a,b)\\ =\sup _{a \in A} d(a,B)\]

\(a \in A\)との距離\(d(a,B)\)を測り、それを最も「大きく」するような、上限を取った距離です。

（これらの関数を暫定的に距離と呼んでいますが、一般的な距離の公理を満たすわけではないことに注意です。半距離 semidistanceとも。）

これらは点と点の距離\(d(a,b)\)の一般化です。

\(a\)と一点集合\(B=\{b\}\)の距離は、\(d(a,B) = \inf_{b\in \{b\}}d(a,b) =d(a,b)\)と通常の距離になります。

一点集合同士\(A=\{a\},B=\{b\}\)の距離は、\(d(A,B)=\sup _{a \in\{a\}} d(a,B) = \sup_{a \in\{a\}} d(a,b)=d(a,b)\)と通常の距離に一致します。

1点と集合の距離：1次元

この距離がどういうものなのか、ごく簡単なケースから考えていきましょう。

\(X=\mathbb{R}\)でユークリッド距離を考えます。

\(B=(0,1)\)としましょう。1点\(a=2\)との距離はいくつでしょうか。

感覚的には、1ではないかと想像できますね。実際、\(d(2, (0,1))=1\)です。

下限の定義にさかのぼって、 \(\inf_{b\in (0,1)}d(2,b)=1\)を示しましょう。まず、すべての\(b \in (0,1)\)に対し、\(d(2,b)= 2-b >1\)なので、\(1\)は下界です。

\(1\)が最小の下界であることを示すため、\(c>1\)なる任意の数\(c\)について考えます。\(c > 2\)のときは、\(b=\frac{1}{2} \in B\)で、\(d(2,b) = \frac{3}{2}< c\)となり、\(c\)は下界ではありません。\(1<c \leq 2\)のとき、\( b = 1- \frac{c-1}{2}\)とすれば、\( 0<1-\frac{1}{2}\leq b<1\)なので、\(b \in B\)です。かつ、\(d(2,b)= 2-(1- \frac{c-1}{2}) = \frac{c+1}{2}<c\)なので、\(c\)は下界ではありません。よって、\(1\)は最小の下界であり、\(d(2,(0,1))=1\)が示せました。

距離の定義で、最小値\(\min \)でなく、下限\(\inf\)で考えたのは、今回の例のように最小値が存在するとは限らないからです。開区間\((0,1)\)には、\(2\)に近い点は、\(0.9,0.99,\dots\)と無数に存在しますが、\(1\)は\((0,1)\)上の点ではないわけですね。

同様に考えると、原点との距離は\(d(0, (0,1))=0\)となります。

\(a= \frac{3}{2}\)と区間の組み合わせ\(B=[0,1] \cup (3,4)\)の距離はどうでしょうか。

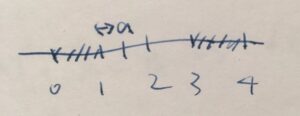
考え方としては、\(\frac{3}{2}\)に最も近い\(B\)の要素はどこか予測できます。

\(d(\frac{3}{2},B)= \frac{1}{2}\)となります。\((3,4)\)の区間は、相対的に遠いので無視できますね。\([0,1]\)との距離を考えると、\(b=1\)のときが最も近いです。したがって、\(d(\frac{3}{2},[0,1]) = \inf_{b \in [0,1]} d(\frac{3}{2},1) = \min_{b \in [0,1] } (\frac{3}{2}-b)= \frac{1}{2}\)となるわけです。

集合間の距離：1次元

集合間の距離は、点と集合の距離を計算し、その上限を取ることで求められます。

例として、\(A = [0,1],B=[2,3]\)のケースを考えましょう。

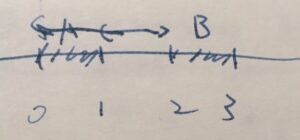
結論としては、\(d(A,B)= 2\)となります。

まず、\(a \in A\)を任意の要素として、\(d(a,B)\)を計算しましょう。\(2\)が\(B\)の中で最も近い要素なので、\(d(a,B)= 2-a\)です。

こうして得た点と集合の距離を、\(A\)について上限を取れば、\(d(A,B)=\sup _{a \in A} d(a,b)= \sup_{a \in [0,1]} (2-a)=2\)と求めることができました。

最初に\(A\)の要素\(a\)を決めて、最短距離\(d(a,B)\)を測りきってしまう。その後、それを最も大きくするような距離が\(d(A,B)\)というわけです。

重複があるケースとして、\(A = [0,2],B=[2,3]\)を考えます。

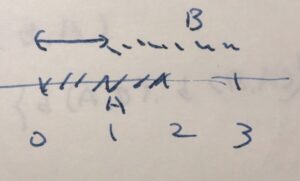
\(a\in A\)とすると、重複がある部分では距離が0になりますが、そうでない部分は距離があります。

\[ d(a,B)= \left\{ \begin{array}{lr} 1-a && (0\leq a<1) \\ 0 && (1 \leq a\leq 2) \end{array} \right. \]

その上限を取れば、集合間の距離は\(d(A,B) = 1\)となりました。\(a=0\)が最も遠い部分というわけです。

包含関係となっているケース、\(A=(0,1),B=(-1,2)\)の距離を考えてみましょう。

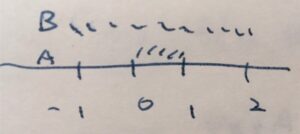
\(a \in A\)とすると、\(A \subset B\)より\(a \in B\)であるため、\(d (a,B)= \inf _{b\in B}d(a,b)=d(a,a)=0 \)となります。したがって、その上限を取っても\(d(A,B)=0\)となります。

この例に限らず、一般に\(A \subset B\)ならば、\(d(A,B)=0\)となるわけです。すっぽり含まれているときは、距離を0と考えるわけですね。

（この逆：\(d(A,B)=0\)だからといって、\(A \subset B\)とは必ずしも言えません。例えば、\(A=[0,1], B=(0,1)\)を考えればわかります。一般には、\(d(A,B)=0\)ならば閉包が\(\overline{A} \subset \overline{B}\)となることが知られています。）

注意したいのは、\(d(A,B)\)が0なのであって、順序を変えた\(d(B,A)\)は0ではありません。これらは基準が異なります。

実際、\(b \in B\)として、

\[ d(b,A)= \left\{ \begin{array}{lr} -b && (-1< b<0) \\ 0 && (0 \leq b\leq 1) \\ b-1 && (0 < b< 2)\end{array} \right. \]

です。この\(B\)に関する上限を取れば、\(d(B,A)=1\)となりました。

\(d(A,B)=0, d(B,A)=1\)であり、この「距離」は対称性を持たないわけです。

対称性を持たせるために、

\[d_{\mathrm{H}}(A,B) := \max\{ d(A,B),d(B,A)\}\]

という距離を考えることがあります。これはハウスドルフ距離（Hausdorff distance）と呼ばれるものです。

\(A=(0,1),B=(-1,2)\)のケースならば、0と1の大きい方なので、\(d_{\mathrm{H}}(A,B)=1\)ですね。

ユークリッド空間の有界閉集合に対し、ハウスドルフ距離を定めると、それは完備な距離空間になることが知られています。

集合間の距離：2次元の例

簡単にですが、2次元\(\mathbb{R}^2\)の例を紹介しておきましょう。

\(B (a,r)\)を中心\(a\)、半径\(r\)の円の内側とします。

\(A=B((0,0),1), B=B((0,1),2)\)の距離はどうなるでしょうか。

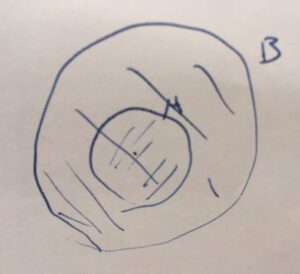
\(A\subset B\)に注意すれば、\(d(A,B)=0\)です。

また、\(d(B,A)=1\)ですね。\(d(b,A)\)は\(A\)の円周上の点との比較になります。その距離が最も大きくなるのは、半径の差：1になるときですね。

\(A=B((0,0),1), B=B((3,0),1)\)の距離\(d(A,B)\)はどうなるでしょうか。

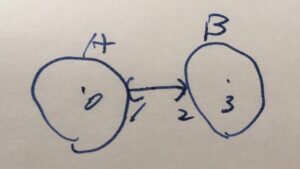
\(d(A,B)=1\)ですね。

\(a=(a_1,a_2) \in A\)とすると、\(a\)と\(B\)の中心\((3,0)\)を結ぶ直線上で、かつ\(B\)の円周上の点が、\(a\)との距離を最短にします。したがって、中心との距離を取って半径を引けば、\(d(a,B)= d((a_1,a_2),(3,0) )-1\)です。これを最大化するのは\((a_1,a_2)=(1,0)\)のときで、したがって\(d(A,B) = 2-1 =1\)となりました。

以上、一点と集合の距離、集合間の距離とは何か、ユークリッド空間を例に紹介してきました。

これは\(A \subset B\)ならば\(d(A,B)=0\)となるような距離で、\(B\)に\(A\)がどれだけ近いかを表しています。近づき具合を表現すれば、アトラクターが定義できます。一般的な扱いは難しいので、まずは1次元の例、点と集合の距離から理解すると良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。