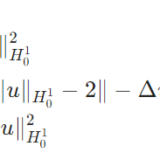どうも、木村(@kimu3_slime)です。
今回は、反応拡散方程式の力学系で\(L^2\)の吸収集合が存在することの証明を紹介します。
反応拡散方程式のL^2における力学系
\(\Omega \subset \mathbb{R}^N\)をなめらかな有界領域とし、
\[\frac{\partial u}{\partial t} -\Delta u =f(u)\]
\[u(t,x)=0\quad(x\in \partial \Omega)\]
\[u(0,x)=u_0(x)\]
という偏微分方程式を考えましょう。この形の方程式は、一般に反応拡散方程式(reaction-diffusion equation)と呼ばれます。\(f(s)=0\)のときとして、熱方程式(拡散方程式)を含んでいます。
以降、(もう少し一般的に扱えますが、単純化のため)非線形項が\(f(s)=s\)や\(f(s)=s-s^3\)のケースを扱いましょう。\(f(s)=s-s^3\)で、1次元(\(N=1\))のケースは、チェイフィー-インファンテ方程式(Chafee-Infante equation)と呼ばれています。
この方程式を弱形式として捉えると、初期条件\(u_0 \in L^2\)に対し、\(u(t) \in L^2\)となる解が一意に存在することが知られています。つまり、抽象力学系\((L^2,(S(t)))\)が定まるわけです。
この形の方程式は、熱方程式と同様の散逸的な挙動を見せます。つまり、グローバルアトラクターの存在を示すことができます。
そのためには、\(L^2\)にコンパクトな吸収集合が存在することを示せば良いです。今回は一旦コンパクト性を保留し、\(L^2\)の吸収集合が存在することを示しましょう。
吸収集合の存在
吸収集合として、「\(u_0 \in L^2\)に対し、「\(t \geq t_0\)ならば\(\|u(t)\|_{L^2} \leq R\)」を満たす\(t_0\)が存在する」ような\(R\)が存在することを示していきましょう。
どんな初期値も、ある程度時間が経てば、\(L^2\)ノルムの大きさが初期値によらず一定以下となるわけです。
弱形式で方程式を書くと
\[\frac{d u}{d t} -\Delta u =u-u^3\]
ですが、ここで両辺に\(u\)をかけて空間について積分しましょう。\(\langle \frac{du}{dt},u\rangle = \frac{1}{2} \frac{d}{dt}\|u\|_{L^2}^2 \)となること、境界で値が0であることに注意して部分積分すれば、
\[ \frac{1}{2} \frac{d}{dt}\|u\|_{L^2}^2 +\|u\|_{H_0^1}^2 = \int_\Omega (u^2-u^4 )dx\]
となります。\(\|u\|_{H_0^1}=\|\nabla u\|_{L^2} \)は簡略化された\(H^1\)ノルムです。
右辺を評価していきましょう。
一般に、\(f(s)s= s^2-s^4 \leq 1- \frac{1}{2}s^4\)となります。差を取れば、\(1- \frac{1}{2}s^4-(s^2-s^4)= \frac{1}{2}(s^4-2s^2)+1 = \frac{1}{2}(s^2-1)^2+\frac{1}{2} \geq 0\)となるので。
したがって、さらに4乗の項を落とせば、右辺は
\[\begin{aligned} &\int_\Omega (u^2-u^4 )dx \\ &\leq \int_\Omega (1-\frac{1}{2}u^4 )dx \\ & \leq\int_\Omega 1dx \\ &=\mu(\Omega) \end{aligned}\]
となります。\(\mu(\Omega)\)は\(\Omega\)の測度(\(N=2\)ならば面積)です。
また、\(\Omega\)は有界なので、ポアンカレの不等式\( \|u\|_{L^2}^2 \leq C_1\|u\|_{H_0^1}\)を満たす\(u\)に依存しない\(C_1 >0\)が存在します。
以上をまとめれば、
\[ \frac{d}{dt}\|u\|_{L^2}^2 +\frac{2}{C_1}\|u\|_{L^2}^2 \\ \leq \frac{d}{dt}\|u\|_{L^2}^2 +\frac{2}{C_1}\|u\|_{H_0^1}^2 \\ \leq 2\mu (\Omega)\]
です。これは微分不等式の単純な形で、グロンウォールの不等式
\[\frac{du}{dt} \leq au+b\]
を満たすならば、
\[u(t) \leq (u(0)+\frac{a}{b})e^{at} – \frac{b}{a} \]
を満たす。
が利用できます。記号が重複しますが、\(u(t):=\|u(t)\|_{L^2} ^2\)、\(a= -\frac{2}{C_1}\)、\(b= 2\mu (\Omega)\)として適用しましょう。
\[\|u(t)\|_{L^2} ^2 \leq (\|u_0\|_{L^2}^2 -\frac{1}{C_1\mu(\Omega)})e^{-\frac{2}{C_1}t} +\frac{C_1 \mu(\Omega)}{2} \\ \leq \|u_0\|_{L^2}^2 e^{-\frac{2}{C_1}t} +C_1 \mu(\Omega)\]
です。ここで、\(\|u_0\|_{L^2}^2e^{-\frac{2}{C_1}t} =C_1 \mu(\Omega)\)となるのは、\(t_0:= \frac{C_1}{2}\log\frac{ \|u_0\|_{L^2}^2}{C_1 \mu (\Omega)} \)のときです。
負の指数を持つ指数関数は単調減少なので、\(t \geq t_0\)ならば
\[\|u(t)\|_{L^2} ^2 \leq \|u_0\|_{L^2}^2 e^{-\frac{2}{C_1}t} +C_1 \mu(\Omega)\\ \leq 2C_1 \mu(\Omega)\]
で、\(R =\sqrt{2C_1 \mu (\Omega)}\)とおけば、
\[\|u_0\|_{L^2} \leq R\]
となりました。\(R\)は\(u_0\)に依存せず、\(t_0\)は\(u_0\)に依存して決まります。
以上により、\(B:=\{v\in L^2 \mid \|v\|_{L^2} \leq R\}\)は反応拡散方程式の力学系の吸収集合であることが示せました。
一様な評価
\(L^2\)にコンパクトな吸収集合が存在することを示すには、レリッヒ・コンドラショフの定理より、\(H_0 ^1\)における有界な吸収集合が存在することを示せば良いです。
その準備として、「\(t \geq t_0\)ならば\(\int_{t}^{t+1} \|u(s)\|_{H_0 ^1}^2 ds \leq R_1\)」を満たす\(R_1\)が存在することを示しておきましょう。
さきほど導いた不等式
\[ \frac{1}{2} \frac{d}{dt}\|u\|_{L^2}^2 +\|u\|_{H_0^1}^2 \leq \mu(\Omega)\]
から始めましょう。これを\(s\)について\(t\)から\(t+1\)まで積分すれば、
\[\begin{aligned} & \int_t ^{t+1}\|u(s)\|_{H_0^1}^2 ds\\ &\leq \int_{t}^{t+1} \mu(\Omega) -\frac{1}{2} \frac{d}{dt}\|u(s)\|_{L^2}^2 ds \\&= \mu(\Omega) -[\frac{1}{2}\|u(s)\|_{L^2}^2]_{s=t}^{s=t+1} \\ &\leq \mu(\Omega)+\frac{1}{2} \|u(t)\|_{L^2}^2 \end{aligned}\]
したがって、さきほどの評価と合わせれば、\(t \geq t_0\)のとき、
\[\begin{aligned} & \int_t ^{t+1}\|u(s)\|_{H_0^1}^2 ds\\ &\leq \mu(\Omega)+\frac{1}{2} \|u(t)\|_{L^2}^2 \\ &\leq \mu(\Omega)+\frac{1}{2} R^2 \end{aligned}\]
なので、\(R_1 :=\mu(\Omega)+\frac{1}{2} R^2 \)と置けば不等式が示せました。
以上、反応拡散方程式の力学系で\(L^2\)の吸収集合が存在することの証明を紹介してきました。
方程式に\(u\)をかけて積分し、非線形項を切り落とすことで、グロンウォールの不等式に持ち込んで示せましたね。
\(H_0^1\)における有界な吸収集合の存在については、別記事にて紹介予定です。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)