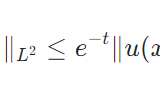どうも、木村(@kimu3_slime)です。
今回は、連続関数のなす空間がL^pノルムで完備でないことを示す例を紹介します。
完備でないことを示す例
1次元の区間\((-1,1)\)における連続関数のなす線形空間を\(C^0\)としましょう。そして積分によるノルム(\(L^p\)ノルム)
\[\|f\|_{L^p}= (\int_{-1}^1 |f(x)|^p dx)^{\frac{1}{p}}\]
ただし\(1\leq p < \infty\)を考えます。このノルムによって\(C^0\)はノルム空間となります。
この連続関数のなすノルム空間\(C^0\)は、完備ではありません。
そのことを示す例として、
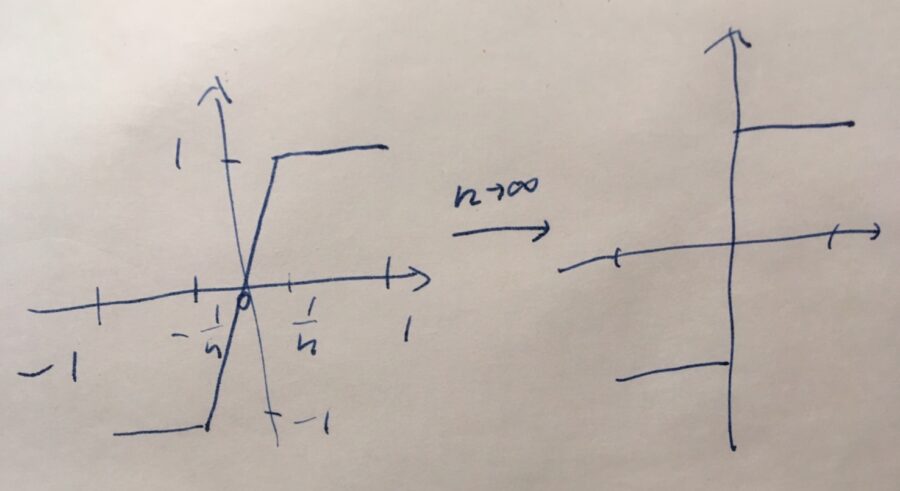
\[ f_n(x)= \left\{ \begin{array}{lr} -1 && (-1 < x \leq -\frac{1}{n}) \\ nx && ( -\frac{1}{n}<x \leq \frac{1}{n}) \\ 1&& ( \frac{1}{n}<x < 1) \end{array} \right. \]
という関数列\((f_n)_{ n \geq 1}\)を考えましょう。これらの関数は、すべて連続です \(f_n \in C^0\)。
距離空間が完備であるとは、どんなコーシー列も収束することでした。
今回は、\((f_n)_{ n \geq 1}\)がコーシー列であるにもかかわらず、(連続関数に)収束しないことを示します。
コーシー列であること
まず、\(n >m\)として、ノルムの差\(\|f_n-f_m\|_{L^p}\)を評価してみましょう。積分を計算するため、場合分けして値を調べます。
\(-1<x \leq – \frac{1}{m}\)または\(\frac{1}{m}<x <1\)のとき、\(f_n(x),f_m(x)\)はともに\(-1\)または\(1\)で一致するので、\(|f_n(x)-f_m(x)|=0\)です。
\(-\frac{1}{m}<x \leq \frac{1}{m}\)のとき、絶対値の三角不等式と、関数の絶対値は1を超えないことから、
\[\begin{aligned} &|f_n(x)-f_m(x)| \\ &= |nx-mx|\\ &\leq |nx|+|mx|\\ &\leq 1+1 \\&\leq 2\end{aligned}\]
となります。したがって、
\[\begin{aligned} & \|f_n-f_m\|_{L^p}^p \\ &=\int_{-1}^{-\frac{1}{m}}|f_n(x)-f_m(x)|^p dx +\int_{-\frac{1}{m}}^{\frac{1}{m}}|f_n(x)-f_m(x)|^p dx \\&\quad+\int_{-1}^{-\frac{1}{m}}|f_n(x)-f_m(x)|^p dx \\ &\leq \int_{-\frac{1}{m}}^{\frac{1}{m}} 2^p dx \\ &= \frac{2^{p+1}}{m}\end{aligned}\]
となり、\(m\)が大きくなればこの差は小さくなっていきます。
この事実を用いて、\((f_n)_{ n \geq 1}\)がコーシー列であることを示しましょう。
\(\varepsilon >0\)を任意の正の実数とします。これに対し、\(N\)を\(\frac{2^{p+1}}{\varepsilon ^p}<N\)を満たす自然数としましょう。言い換えれば、\(\frac{2^{p+1}}{N} <\varepsilon ^p\)です。
\(n,m \geq N\)であるような自然数\(n,m\)を考えましょう。\(n >m\)のとき、さきほど示した計算から
\[\begin{aligned} & \|f_n-f_m\|_{L^p} \\ &= (\frac{2^{p+1}}{m})^{\frac{1}{p}} \\ &\leq (\frac{2^{p+1}}{N})^{\frac{1}{p}} \\ & < (\varepsilon ^p)^{\frac{1}{p}} \\ &= \varepsilon \end{aligned}\]
が成り立ちます。\(m \geq n\)のときも全く同様です。よって、\((f_n)_{ n \geq 1}\)はコーシー列です。
収束しないこと
\((f_n)_{ n \geq 1}\)は\(C^0\)において\(L^{p}\)ノルムでは収束しません。
それを示すために、仮に収束したと、\(\lim_{n\to \infty}\|f_n-f\|_{L^{p}}=0\)を満たす連続関数\(f\)が存在したとしましょう(背理法)。
この\(f\)は、冒頭の図で示したような連続でない関数になることを示します。
まず、\(-1<a <0\)を満たす\(a\)について考えると、
\[\begin{aligned} &\int_{-1}^a |f_n(x)-f(x)|^p dx\\ &\leq \int_{-1}^1 |f_n(x)-f(x)|^p dx \\&= \|f_n-f\|_{L^p}^p \\&\to 0 \quad(n\to \infty) \end{aligned}\]
となります。\(n\)が大きいとき、\(a<-\frac{1}{n}\)となるので、\(-1<x<a\)において\(f_n(x) =-1\)です。つまり、\(\int_{-1}^a |-1-f(x)|^p dx=0\)でなければなりません(そうでないと、\(\lim_{n\to \infty}\|f_n-f\|_{L^{p}}=0\)に矛盾する)。
したがって、被積分関数は非負なので、積分の中身も0でなければならず、\(-1<x<a\)のとき\(f(x)=-1\)です。\(a\)は\(-1<a <0\)を満たすならどんな数でもこの議論ができるので、\(-1<x<0\)のとき\(f(x)=-1\)と言えます。
全く同様に議論で、\(0<x<1\)のとき\(f(x)=1\)です。
この関数\(f\)は、\(x=0\)において連続ではありえません。これは連続関数\(f\)が存在するという仮定に矛盾します。
よって、\((f_n)_{ n \geq 1}\)は\(C\)において\(L^{p}\)ノルムでは収束しないことが示せました。
完備性の考察
連続関数\(C^0\)ではなく、(ルベーグの意味で)\(p\)乗可積分な関数のなす空間\(L^p\)において、積分ノルム(\(L^p\))を考えると、完備になります。
実際、今回示した関数列の\(L^p\)ノルムでの極限は、\(C\)においては収束しませんが、
\[ f(x)= \left\{ \begin{array}{lr} -1 && (-1<x\leq 0) \\ 1 && (0<x< 1) \end{array} \right. \]
は\(p\)乗可積分で、\(f\in L^p\)です。
基本的には、可積分関数のなす空間\(L^p\)は、連続でない関数を含む、連続関数のなす空間\(C\)より広い空間です。
またこの結果を、連続関数のなす空間は常に完備ではない、と誤解しないように注意しましょう。考えるノルムが\(L^p\)ノルムの場合に、完備でないという結果です。
実際、端点を含めた区間において、上限ノルム
\[\|f\|_{C^0} := \sup_{-1 \leq x \leq 1}|f(x)|\]
を考えれば、このノルムについて\(C^0\)は完備です。連続関数列の一様収束極限は連続に関連する結果ですね。
一般に、有界な連続関数のなす空間\(B^0\)において、上限ノルムを考えると完備になります。
ノルムによって完備性を持ったり持たなかったりするという状況は、有限次元ではありえません。
実際、有限次元のノルム空間は、必ず完備になります。また、すべてのノルムが同値となります。
つまり、関数空間\(C\)や\(L^p\)が無限次元であること特有の状況を、今回の例は示しているわけです。
また、(無限次元の空間における)完備性を考えるときには、空間だけでなく、何のノルムを考えているか、何のノルムについて完備なのかが大事であることを示す例と言えます。
\(L^p\)ノルムによる関数列の収束を考えることは、フーリエ級数展開や偏微分方程式において重要です。
矩形波のように、連続でない(\(C^0\)の要素でない)が、2乗可積分(\(L^2\)の要素である)な関数は、三角関数によって近似すること、フーリエ級数展開ができます。

このような関数を近似するとき、関数の距離の基準は最大値を測る上限ノルムでなく、積分的な違いを測る\(L^2\)ノルムです。
積分による関数列の収束を考えるとき、連続関数\(C^0\)だと取りこぼしがありうる(完備でない)ので、可積分関数\(L^p\)という広めの(完備な)空間を考える意義があるというわけです。
以上、連続関数のなす空間がL^pノルムで完備でないことを示す例を紹介してきました。
関数解析や偏微分方程式の分野では、\(L^p\)ノルムによる収束をしばしば考えますが、そのモチベーションのひとつとして今回の例を通じた完備性への意識が伝われば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)
こちらもおすすめ
フーリエ級数の収束条件:L^2収束、一様収束、不連続点での値