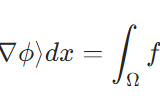ソボレフ空間W^{k,p}・H^kが線形、ノルム、内積空間となることの証明

どうも、木村（@kimu3_slime）です。

今回は、ソボレフ空間が線形、ノルム、内積空間となることの証明を紹介します。

ソボレフ空間とは
線形空間となること
ノルムの定義を満たすこと
内積の定義を満たすこと
こちらもおすすめ

ソボレフ空間とは

まず、前提知識を確認しておきます。ソボレフ空間とは、

\[W^{k,p}(\Omega):=\{u \mid すべての多重指数\alpha に対し、\\0 \leq |\alpha| \leq k ならば D^{\alpha} u \in L^p(\Omega)\}\]

\[H^k(\Omega) := W^{k,2}(\Omega)\]

という集合に、関数の和とスカラー倍という演算を定めたものです。

\(W^{k,p}\)に対してはノルム

\[\|u\|_{W^{k,p}}:=(\sum_{0 \leq |\alpha| \leq k} \|D^{\alpha}u\|_{L^p}^p)^\frac{1}{p}\]

を、\(H^k\)に対しては内積

\[\langle u,v\rangle_{H^k}:=\sum_{0 \leq |\alpha| \leq k} \langle D^\alpha u, D^{\alpha} v\rangle_{L^2}\]

を定義します。

\(1\leq p < \infty\)のとき、\(W^{k,p}\)が線形空間となること、上で定義した関数が、ノルム、内積の定義を満たすことを証明していきましょう。

関数空間\(L^p\)が線形空間であること、

\[\|u\|_{L^p}= (\int_\Omega |u(x)|^p dx )^\frac{1}{p}\]

\[\langle u,v\rangle_{L^2} = \int _\Omega u(x)v(x)dx\]

がノルム、内積の定義を満たすことは前提とします。

線形空間となること

\(W^{k,p} \subset L^p\)なので、\(W^{k,p}\)が\(L^p\)の部分空間として線形空間になること、すなわち

すべての\(u,v \in W^{k,p}\)、\(\lambda \in \mathbb{R}\)に対し、\(\lambda u +v \in W^{k,p}\)

を示しましょう。

まず、\(L^{p}\)は線形空間なので、\(\lambda u + v \in L^{p}\)です。

これが\(\lambda u +v \in W^{k,p}\)となることを示すには、\(k\)階まですべて弱微分可能で、導関数が\(L^p\)に属することを示せば良いです。

\(\alpha\)を\(0 \leq |\alpha | \leq k\)を満たす多重指数としましょう。\(D^{\alpha} (\lambda u +v ) =\lambda D^{\alpha} u + D^{\alpha}v\)となること（弱微分の線形性）を示します。

\(|\alpha|\)回弱微分可能とは、すべての\(\phi \in C_c ^\infty (\Omega)\)に対し、

\[\int _{\Omega} u (D^{\alpha}\phi) dx \\= (-1)^{|\alpha|}\int_{\Omega} (D^{\alpha}u) \phi dx\]

を満たすことでした。

したがって、すべての\(\phi \in C_c ^\infty (\Omega)\)に対し、積分の線形性に注意すれば、

\[\begin{aligned} &\int_{\Omega} (\lambda u +v) (D^{\alpha} \phi)dx \\ &= \lambda \int_{\Omega} u (D^{\alpha} \phi) dx\\&\quad +\int_{\Omega} v (D^{\alpha} \phi)dx \\ &= (-1)^{|\alpha|}\lambda \int_{\Omega} (D^{\alpha}u) \phi dx\\&\quad +(-1)^{|\alpha|}\int_{\Omega} (D^{\alpha} v)\phi dx \\ &=(-1)^{|\alpha|}\int_{\Omega} (\lambda D^{\alpha} u+D^{\alpha} v)\phi dx \end{aligned}\]

となり、\(D^{\alpha} (\lambda u +v ) =\lambda D^{\alpha} u + D^{\alpha}v\)が示せました。

\(u,v \in W^{k,p}\)より、\(D^{\alpha} u, D^{\alpha} v \in L^{p}\)で、\(L^{p}\)は線形空間なので\(\lambda D^{\alpha} u + D^{\alpha}v \in L^p\)です。したがって、\(\lambda u + v \in W^{k,p}\)となります。

以上により、

すべての\(u,v \in W^{k,p}\)、\(\lambda \in \mathbb{R}\)に対し、\(\lambda u +v \in W^{k,p}\)

すなわち、\(W^{k,p}\)が線形空間となることが示せました。

ノルムの定義を満たすこと

\[\|u\|_{W^{k,p}}:=(\sum_{0 \leq |\alpha| \leq k} \|D^{\alpha}u\|_{L^p}^p)^\frac{1}{p}\]

がノルムの定義

\(V\)を線形空間とする。1変数関数\(\| \cdot \| :V \to \mathbb{R}\)は、次を満たすときノルムと呼ばれる。

任意の\(a,b\in V\)、\(\lambda \in \mathbb{R}\)に対し、

(1) 正定値性：\(\|a\| \geq 0\)。\(a= 0\)は\(\|a\| = 0\)と同値である。

(2) 斉次性：\(\|\lambda a\| = |\lambda| \| a\| \)

(3) 三角不等式（劣加法性）：\(\|a+b\| \leq \|a\|+ \|b\|\)

を満たすことを示しましょう。

正定値性について。

まず、\(L^{p}\)ノルムの正定値性から、\(\|D^{\alpha}u\|_{L^p} \geq 0\)です。非負の数をべき乗しても正\(\|D^{\alpha}u\|_{L^p}^p \geq 0\)で、非負の数の有限個の和は正\(\sum_{0 \leq |\alpha| \leq k}\|D^{\alpha}u\|_{L^p}^p \geq 0\)、再び非負の数をべき乗しても非負\((\sum_{0 \leq |\alpha| \leq k} \|D^{\alpha}u\|_{L^p}^p)^\frac{1}{p} \geq 0\)です。

\(u=0\)と仮定しましょう。このとき、すべての弱微分は\(D^{\alpha}u =0\)となります。なぜなら、

\[\int _{\Omega } 0 (D^{\alpha}\phi) dx \\= (-1)^{\alpha} \int_{\Omega} (D^{\alpha}u )\phi dx \]

は、\(D^{\alpha}u =0\)とすれば両辺0で成り立つからです。したがって、\(L^p\)ノルムの正定値性から\(\|D^{\alpha}u\|_{L^p}=0\)で、そのべきと和も\(\|u\|_{W^{k,p}}=0\)となります。

逆に、\(\|u\|_{W^{k,p}}=0\)としましょう。両辺を\(p\)乗すれば\(\sum_{0 \leq |\alpha| \leq k}\|D^{\alpha}u\|_{L^p}^p =0\)です。非負の数の和が0になるということは、左辺の項はすべて0でなければなりません、すなわち\(\|D^{\alpha}u\|_{L^p}^p=0\)です。両辺を\(\frac{1}{p}\)乗すると、\(\|D^{\alpha}u\|_{L^p}=0\)です。\(\alpha =(0,\dots,0)\)のケースを考えれば、\(\|u\|_{L^p}=0\)となっています。よって、\(L^p\)ノルムの正定値性から、\(u=0\)と言えました。

斉次性について。

弱微分の線形性、\(L^p\)ノルムの斉次性、和の線形性を用いれば、

\[\begin{aligned} & \|\lambda u\|_{W^{k,p}}\\ &= (\sum_{0 \leq |\alpha| \leq k} \|D^{\alpha} (\lambda u)\|_{L^p}^p)^\frac{1}{p} \\&= (\sum_{0 \leq |\alpha| \leq k} \|\lambda (D^{\alpha} u)\|_{L^p}^p)^\frac{1}{p} \\&= (\sum_{0 \leq |\alpha| \leq k} |\lambda|^p \| (D^{\alpha} u)\|_{L^p}^p)^\frac{1}{p} \\&= (|\lambda|^{p} \sum_{0 \leq |\alpha| \leq k} \| (D^{\alpha} u)\|_{L^p}^p)^\frac{1}{p} \\&= |\lambda |(\sum_{0 \leq |\alpha| \leq k} \| (D^{\alpha} u)\|_{L^p}^p)^\frac{1}{p} \\&= |\lambda|\|u\|_{W^{k,p}}\end{aligned}\]

と示せます。

三角不等式について。

弱微分の線形性、\(L^p\)ノルムの三角不等式、\(p\)ノルムの三角不等式

\[(|a_1+b_1|^p+\cdots +|a_n+b_n|^p)^{\frac{1}{p}} \\ \leq (|a_1|^p+\cdots+|a_n|^p)^{\frac{1}{p}} +(|b_1|^p+\cdots+|b_n|^p)^{\frac{1}{p}} \]

を用いて

\[\begin{aligned} &\|u+v\|_{W^{k,p}} \\ &=(\sum_{0 \leq |\alpha| \leq k} \|D^{\alpha}(u+v)\|_{L^p}^p)^\frac{1}{p} \\&=(\sum_{0 \leq |\alpha| \leq k} \|D^{\alpha}u+D^{\alpha}v\|_{L^p}^p)^\frac{1}{p} \\ &\leq [\sum_{0 \leq |\alpha| \leq k} (\|D^{\alpha}u\|_{L^p}+\|D^{\alpha}v\|_{L^p})^p]^\frac{1}{p} \\&\leq (\sum_{0 \leq |\alpha| \leq k} \|D^{\alpha}u\|^p_{L^p})^{\frac{1}{p}}+ (\sum_{0 \leq |\alpha| \leq k}\|D^{\alpha}v\|_{L^p}^p)^\frac{1}{p} \\&= \|u\|_{W^{k,p}}+\|v\|_{W^{k,p}} \end{aligned}\]

と示せます。

以上により、\(W^{k,p}\)はノルム空間です。

内積の定義を満たすこと

\(H^k =W^{k,2}\)については、

\[\langle u,v\rangle_{H^k}:=\sum_{0 \leq |\alpha| \leq k} \langle D^\alpha u, D^{\alpha} v\rangle_{L^2}\]

が内積の定義

\(V\)を線形空間とする。2変数関数\(\langle \cdot,\cdot \rangle :V\times V \to \mathbb{R}\)は、次を満たすとき内積と呼ばれる。

任意の\(a,b\in V\)、\(\lambda \in \mathbb{R}\)に対し、

(1) 対称性：\(\langle a,b\rangle =\langle b,a\rangle\)

(2) （二重）線形性：\(\langle \lambda a+c,b\rangle = \lambda \langle a,b\rangle +\langle c,b\rangle\)

(3) 正定値性：\(\langle a,a\rangle \geq 0\)。\(a\neq 0\)ならば\(\langle a,a\rangle > 0\)。

を満たすことを示しましょう。

対称性について。

\(L^2\)内積の対称性から、

\[\begin{aligned} &\langle u,v\rangle_{H^k} \\ &= \sum_{0 \leq |\alpha| \leq k} \langle D^\alpha u, D^{\alpha} v\rangle_{L^2}\\&= \sum_{0 \leq |\alpha| \leq k} \langle D^\alpha v, D^{\alpha} u\rangle_{L^2} \\&=\langle v,u\rangle_{H^k} \end{aligned}\]

となります。

二重線形性について。

弱微分の線形性、\(L^2\)内積の二重線形性、和の線形性から、

\[\begin{aligned} &\langle \lambda u+w,v\rangle_{H^k} \\ &= \sum_{0 \leq |\alpha| \leq k} \langle D^\alpha (\lambda u+ w), D^{\alpha} v\rangle_{L^2}\\&= \sum_{0 \leq |\alpha| \leq k} \langle \lambda (D^\alpha u )+ w, D^{\alpha} v\rangle_{L^2} \\&= \sum_{0 \leq |\alpha| \leq k} (\lambda \langle D^\alpha u , D^{\alpha} v\rangle_{L^2} + \langle w, D^{\alpha} v\rangle_{L^2}) \\ &=\lambda \sum_{0 \leq |\alpha| \leq k} \langle D^\alpha u , D^{\alpha} v\rangle_{L^2} +\sum_{0 \leq |\alpha| \leq k} \langle w, D^{\alpha} v\rangle_{L^2} \\&=\lambda \langle u,v\rangle_{H^k}+\langle w,v\rangle_{H^k} \end{aligned}\]

と示せます。

正定値性について。

\(L^2\)内積の正定値性から、\(\langle D^\alpha u, D^{\alpha} u\rangle_{L^2} \geq 0\)です。非負の数の有限和は非負なので、\(\sum_{0 \leq |\alpha| \leq k} \langle D^\alpha u, D^{\alpha} u\rangle_{L^2} \geq 0\)となります。

\(u \neq 0\)と仮定しましょう。\(L^2\)内積の正定値性から、\(\langle u, u\rangle_{L^2} >0\)です。正の数に非負の数を有限個足しても正なので、\(\sum_{0 \leq |\alpha| \leq k} \langle D^\alpha u, D^{\alpha} u\rangle_{L^2} > 0\)です。

以上により、\(H^k =W^{k,2}\)は内積空間の定義を満たします。

ちなみに、

\[\begin{aligned} & \sqrt{\langle u,u\rangle_{H^k}}\\ &=( \sum_{0 \leq |\alpha| \leq k} \langle D^\alpha u, D^{\alpha} u\rangle_{L^2})^\frac{1}{2} \\&= ( \sum_{0 \leq |\alpha| \leq k} \|u\|^2_{L^2})^\frac{1}{2} \\ &= \|u\|_{H^k}\end{aligned}\]

という関係を満たすので、内積とノルムは対応していて、\(H^k=W^{k,2}\)ノルムは\(H^k\)ノルムから誘導されるものになっています。

以上、ソボレフ空間が線形、ノルム、内積空間となることの証明を紹介してきました。

\(L^p\)空間が線形、ノルム、内積空間であることを知っていれば、手間はかかりますが素直に証明できることです。ぜひ自分の手でも確かめてみてはいかがでしょうか。

木村すらいむ（@kimu3_slime）でした。ではでは。