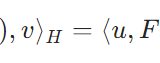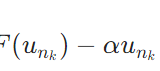対称作用素の作用素ノルムの内積による表示の証明

どうも、木村（@kimu3_slime）です。

今回は、対称作用素の作用素ノルムの内積による表示の証明を紹介します。

定義の確認
証明
こちらもおすすめ

定義の確認

\(H\)をヒルベルト空間（完備なノルム空間）、\(F:H \to H\)を有界線形かつ対称な作用素とします。このとき、その作用素ノルムは内積を使って

\[\|F\|_{B(H,H)} = \sup_{\|u\|_{H}=1} |\langle F(u),u\rangle|\]

と表せる。これが今回示したいことです。

証明

等号の成立を示すために、2つの不等式に分けて示しましょう。

\[\|F\|_{B(H,H)} \geq \sup_{\|u\|_{H}=1} |\langle F(u),u\rangle|\]

\(u \in H\)を\(\|u\|_{H}=1\)を満たす要素とします。このとき、コーシー・シュワルツの不等式と作用素ノルムの定義から

\[\begin{aligned} & |\langle F(u),u\rangle|\\ &\leq \|F(u)\|_H \|u\|_H \\ & \leq \|F\|_{B(H,H)}\|u\|_H^2 \\ &= \|F\|_{B(H,H)} \end{aligned}\]

となります。\( \|F\|_{B(H,H)} \)は上界で、上限は最小の上界なので、

\[\sup_{\|u\|_{H}=1} |\langle F(u),u\rangle| \leq \|F\|_{B(H,H)} \]

が示せました。

\[\|F\|_{B(H,H)} \leq \sup_{\|u\|_{H}=1} |\langle F(u),u\rangle|\]

作用素ノルムの定義より、\(u \in X\)に対し

\[\|F(u)\|_H \leq (\sup_{\|u\|_{H}=1} |\langle F(u),u\rangle|) \|u\|_{X} \]

を示せば良いです。

\(u=0\)のとき、\(F\)の線形性より\(F(u)=0\)、ノルムの正定値性より、不等式は両辺0として成り立ちます。以降では\(u \neq 0\)としましょう。

ノルムと内積の関係を用いて、都合の良い形を作ります。

\[\begin{aligned} &\|F(u)\|_H^2 \\ &= \langle F(u),F(u)\rangle _H \\&= \langle F(u),\frac{\|u\|_H}{\|F(u)\|_H}F(u)\rangle _H \frac{\|F(u)\|_H}{\|u\|_H}\end{aligned}\]

ここで\(v=\frac{\|u\|_H}{\|F(u)\|_H}F(u) \)と置くと、\(\|v\|_H =\frac{\|u\|_H}{\|F(u)\|_H}\|F(u)\|_H =\|u\| \)です。

また一般に、\(u \in H, u \neq 0\)に対し、\(F\)の線形性、上限が上界であることから

\[\begin{aligned} &|\langle F(u),u \rangle| \\ &=|\langle F(\frac{1}{\|u\|_H}u),\frac{1}{\|u\|_H}u \rangle| \|u\|_H^2 \\&\leq (\sup_{\|u\|_{H}=1} |\langle F(u),u\rangle|) \|u\|_{X} ^2 \end{aligned}\]

です。これと内積の線形性、ノルムの二乗の展開（中線定理）を用いて、さきほどの等式を不等式評価すれば、

\[\begin{aligned} &\|F(u)\|_H \\ &= \frac{1}{\|u\|_H}\langle F(u),v\rangle _H\\ &= \frac{1}{4\|u\|_H}( \langle F(u+v),u+v\rangle _H- \langle F(u-v),u-v\rangle _H) \\ & \leq \frac{\sup_{\|u\|_{H}=1} |\langle F(u),u\rangle|}{4\|u\|_H} (\|u+v\|^2_{H}+\|u-v\|_H^2)\\&=\frac{\sup_{\|u\|_{H}=1} |\langle F(u),u\rangle|}{4\|u\|_H} (2\|u\|^2_{H}+2\|v\|_H^2)\\&=(\sup_{\|u\|_{H}=1} |\langle F(u),u\rangle|) \|u\|_H\end{aligned}\]

が示せました。ここでノルムの二乗の展開において、\(F\)の対称性から

\[\begin{aligned} &\langle u,v\rangle_H \\ &= \langle u,\frac{\|u\|_H}{\|F(u)\|_H}F(u)\rangle_H\\&=\langle F(u),\frac{\|u\|_H}{\|F(u)\|_H}u\rangle_H \\&= \langle\frac{\|u\|_H}{\|F(u)\|_H} F(u),u\rangle_H\\&=\langle v,u\rangle_H \end{aligned}\]

が成り立つのを用いていることに注意しましょう。（実内積ならば、この議論に対称性は必要ありません。）

作用素ノルムの定義より、

\[\|F\|_{B(H,H)} \leq \sup_{\|u\|_{H}=1} |\langle F(u),u\rangle|\]

です。

以上により、

\[\|F\|_{B(H,H)} = \sup_{\|u\|_{H}=1} |\langle F(u),u\rangle|\]

が成り立ちます。

以上、対称作用素の作用素ノルムの内積による表示の証明を紹介してきました。

これはコンパクトな対称作用素の固有値の存在を示すための、近似の基礎となります。それについては別記事にて。

木村すらいむ（@kimu3_slime）でした。ではでは。