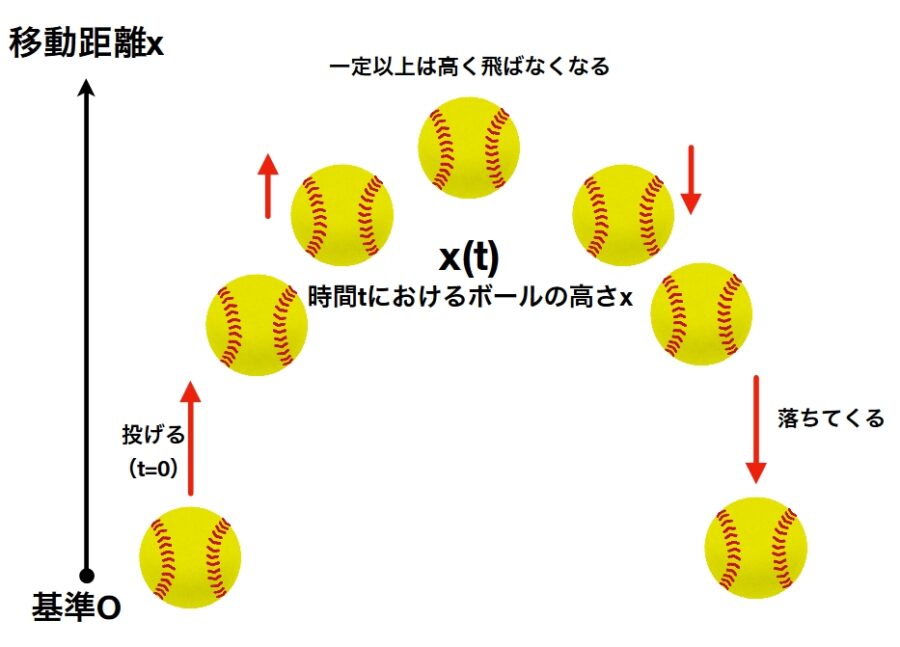
大学数学の基礎として、論理、証明、集合の記事をまとめて紹介します。
大学初年度は教養数学として、微積分学や線形代数学を学ぶことが多いです。それらをきちんと知るためには、数学の言葉遣い、論理・証明・集合の考え方が必要です。
僕は高校までの数学と大学数学の講義や教科書にギャップを感じたのですが、それは以下の内容を独学することで解消されていきました。
論理、証明、集合の内容は、学部1年の講義やカリキュラムにないかもしれませんし、微積分や線形代数を学ぶ上で必須というわけでもありません。しかし、数学の言葉遣いを身につけることは、どんな数学の分野を学ぶ上でも役に立つでしょう。
論理的な考え方
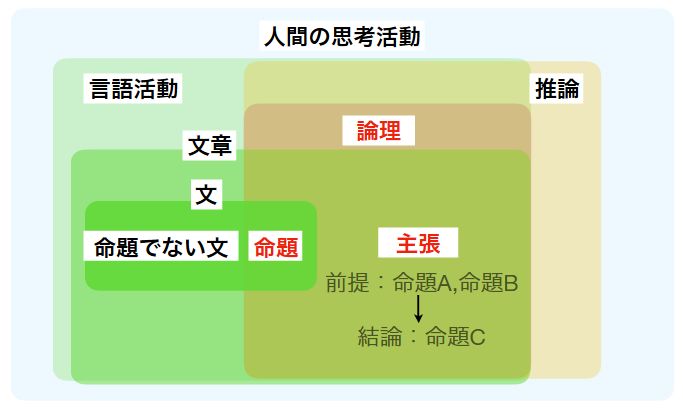
数学の文章を読んだり書いたりする上で欠かせないのが、論理と証明に対する理解です。
数学の議論では、正しいとわかっていること(仮定)から示したいこと(結論)を、少しずつ論理的に証明していきます。
日常用語と違い、数学用語は限られた意味を持ちますが、その約束は定義と呼ばれます。三平方の定理のように、数学的な結果は定理や命題と呼ばれるものです。
高校数学まではあまり意識されませんが、大学数学ではどれも欠かせない用語たちです。まずはこうした用語に馴染んでいきましょう。
大学数学の教科書の読み方、最初に「定義・命題・証明」を知ろう
「自明、明らかである」に気をつけて、疑いながら数学書を読もう
数学の学びを深めるために必要なのは、「わからない」と言える力
厳密さ・証明が現代数学で要求されるのはなぜ? 近代数学の歴史をたどる
論理の用語、記号
数学の議論の基礎になっているのは、論理です。
論理の基本的な用語としては、かつ、または、でない、ならば、同値の意味、それらの組み合わせをまず知りましょう。
大学数学で頻繁に登場し、かつ身につけるまで苦戦するのが、すべての(全称命題)、存在する(存在命題)という考え方です。
これらの考え方は、しばしば記号を使って表されますが、それも知っておくと良いでしょう。
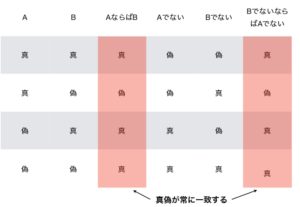
「AならばB」のよくある誤解から学ぶ、論理学入門(対偶、逆、否定、真偽表
記号論理、命題論理入門:覚えるべき論理記号(否定、かつ、または、ならば、同値)とは
述語論理、量化子とは:全称記号(∀)と存在記号(∃)、数学における例と否定
証明の書き方
論理の基本的な用語を知った上で、実際に自分の手で簡単な証明を書けるようになることは大事です。
むしろ、論理の話がよくわからなければ、まずはこれらの具体的な証明の書き方を知ると良いでしょう。
数学の講義や教科書では、複雑な証明を扱うことがあります。それらを部分的にでも理解できるようになるために、ぜひ証明の能力を鍛えましょう。
偶数+奇数はいつでも奇数? 読み解き方、よくある間違いと証明
集合論

論理や証明の能力を基礎として、数学ではさらに集合の言葉を使います。集合論は、現代数学の基礎です。数も空間も関数も、すべて集合として構成されます。論理的な考え方を簡単に表記する上でも、集合の記法は便利です。
高校の集合分野では要素が有限個の集合を扱うことが多いですが、大学数学では数の集合を例として、要素が無限個の集合を扱います。
ベン図を書くだけでは集合の包含関係も説明できないので、そこで論証力が試されます。
集合に関連して、空集合、差集合、直積集合と順序組、集合族、写像と定義域・終域、像と逆像、単射・全射・全単射、2項関係、同値関係、順序関係、空間、商集合、濃度といったキーワードも重要です。
ここでは紹介していませんが、抽象代数:群、環、体、加群の話、位相空間の話はしばしば集合論とセットで学ばれます。
これらは数学全般で登場する概念ですが、他の分野で具体的にどう使われているかを知らないと、ピンと来ないかもしれません。必要に応じて学びましょう。
集合、構造、空間とは何か? ユークリッド空間R^Nを例に考える
well-definedとは:代表元の取り方によらない確認はなぜ必要か
ガリレオのパラドックスとヒルベルトの無限ホテルから感じる、無限集合の性質
無限集合の濃度とは? 写像の全単射、可算無限、カントールの対角線論法
古典論理

今まで紹介してきたのは、数学に必要な論理、形式論理、古典論理、記号論理学と呼ばれるものでした。
それらの分野が生まれる以前から論理の考え方、アリストテレスに端を発する伝統的論理学はあります。それを知らなくても数学はできますが、学ぶと数学や日常において論理を活用する視点を養えるでしょう。
三段論法の分類:叙法(A,E,I,O)と格、形式、妥当な15種とは
教科書
僕は大学1年のとき、松坂「集合・位相入門」を読んで、この記事に書いたような内容が大学数学の理解には欠かせないと気づきました。
ただし、独学するには少し難しいかもしれないので、自分の肌に合う本を選ぶと良いでしょう。
詳しくは:大学入学前に数学を予習したい人におすすめの本・勉強法
ベレ出版 (2016-09-26T00:00:00.000Z)
¥1,584
日本評論社 (2012-08-17T00:00:01Z)
¥1,427 (中古品)
日本評論社 (2008-12-10T00:00:00.000Z)
¥2,717
裳華房 (2020-08-15T00:00:01Z)
¥6,160 (コレクター商品)
Richard Hammack (2019-07-19T00:00:01Z)
¥3,652
岩波書店 (2018-11-07T00:00:01Z)
¥2,860
「集合と位相」をなぜ学ぶのか ― 数学の基礎として根づくまでの歴史
技術評論社 (2018-03-06T00:00:01Z)
¥4,488 (コレクター商品)