どうも、木村(@kimu3_slime)です。
今回は、全単射と逆写像の存在が同値であることの証明、応用を紹介します。
逆写像とは
\(X,Y\)を集合、\(f:X \to Y\)を写像(関数)とします。
写像\(g: Y \to X\)が\(f\)の逆写像(逆関数)(inverse mapping, function)であるとは、「すべての\(x \in X\)に対して\(g(f(x)) =x\)」かつ「すべての\(y \in Y\)に対して\(f(g(y)) =y\)」が成り立つことです。前者の条件は左逆写像、後者の条件は右逆写像とも呼ばれます。
\(f\)に逆写像が存在するとき、\(f\)は可逆である(invertible)と呼びます。また、逆写像はしばしば\(g= f^{-1} \)と表記されます。
例として、\(X = [0,\infty) := \{ x \in \mathbb{R} \mid x \geq 0\}\)、\(Y=[0,\infty) \)、\(f(x)= x^2\)を考えましょう。\(g:Y \to X\)を\(g(y)= \sqrt{y}\)で定めます。
\(x \in X\)として、\(g(f(x))= g(x^2) = \sqrt{x ^2} =x\)です(\(x \geq 0\)に注意)。\(y \in Y\)として、\(f(g(y))= f(\sqrt{y}) = (\sqrt{y}) ^2 = y\)です(平方根の定義)。よって、\(f\)の逆写像は\(g\)であるとわかりました。
逆写像は、いつでも存在するとは限りません。例えば、\(f:\mathbb{R} \to [0,\infty)\)、\(f(x)= x^2\)。
ただし、ある写像の\(f\)の逆写像は、存在するならば唯一つとなります。
また、\(f\)の逆写像が\(g\)ならば、\(g\)の逆写像は\(f\)となります(\((f^{-1})^{-1}= f\) 逆写像の逆写像は元の写像)。
全単射と逆写像の存在が同値であることの証明
では、次の同値条件を証明してみましょう。
\(X,Y\)を集合、\(f:X \to Y\)を写像(関数)とする。
\(f\)が全単射であることと、\(f\)の逆写像\(g\)が存在する(\(f\)が可逆である)ことは同値。
まず、\(f\)を全単射と仮定します。
\(g: Y \to X\)を次のようにして定めましょう。\(f\)は全射であることから、すべての\(y \in Y\)に対して、\(f(x) =y\)となる\(x \in X\)が存在します。これを使って\(g(y) = x\)と定義します。
\(g\)は写像となります(2つ以上の値を取らない)。つまり、与えられた\(y\in Y\)に対し、\(f(x) =y\)となる\(x \in X\)は唯一つです。なぜなら、\(f(x)= f(w) = y\)となったとしましょう。\(f\)の単射性(の対偶)から、\(x= w\)となるからです。
左逆写像となること:\(x \in X\)とします。\(y :=f(x) \)と置くと、\(f(x)=y\)を\(x\)は満たすので、\(g\)の定義から\(g(y)= x\)、つまり\(g(f(x))= x\)です。
右逆写像となること:\(y \in Y\)とします。\(f\)の全射性から\(f(x) =y\)を満たす\(x\)が存在します。\(g\)の定義から、\(g(y)=x\)です。よって、\(f(g(y))= f(x)= y\)となります。
以上により、\(f\)に逆写像\(g\)が存在することがわかりました。
逆に、\(f\)の逆写像\(g\)が存在すると仮定しましょう。
単射性:\(x_1, x_2 \in X\)、\(f(x_1) = f(x_2)\)とします。\(g\)が左逆写像であることから、\(g(f(x_1))= x_1\)、\(g(f(x_2))= x_2\)です。これらを合わせれば、\(x_1 =x_2\)が導かれました。
全射性:\(y \in Y\)とします。\(g\)が右逆写像となることから、\(f(g(y)) =y\)です。\(x=g(y) \)と置くと、\(x \in X\)であり、\(f(x)= y\)を満たすので、\(f\)は全射です。
よって、\(f\)は全単射であると示せました。
応用
全単射と逆写像(逆関数)存在の同値性は、当たり前のように利用される性質です。
\(f\)が全単射であるときは、逆関数は次のようにしても定義されます。つまり、\(f^{-1}(y)\)は、「\(f(x)= y\)を満たす唯一の要素\(x\)」と定義されるわけです。
これが逆関数の定義を満たすことは、さきほどの証明で見た通りです。
また、逆写像を具体的に構成することによって、全単射性を示すことができます。
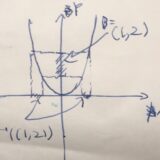
簡単な例ですが、\(f(x)=2x+1\)が\([0,1]\)から\([1,3]\)への全単射であることを示したいとします。
\(y =f(x)\)とおいてこれを\(x\)について解けば、\(x= \frac{1}{2}(y-1)\)です。そこで\(g(y):=\frac{1}{2}(y-1)\)と置きましょう。\(g\)は\([1,3]\)から\([0,1]\)への写像となっています。また、\(g(f(x))= \frac{1}{2}((2x+1)-1)=x\)、\(f(g(y))= 2(\frac{1}{2}(y-1))+1=y\)なので、\(g\)が逆写像であり、\(f\)が全単射であることがわかりました。
以上、全単射と逆写像の存在が同値であることの証明、応用を紹介してきました。
線形代数学では行列が可逆であることと全単射は同値という基本的な性質がありますが、それを含んでいるのが今回の話です。
\(X,Y\)が集合という非常に一般的な条件で成り立つ議論なので、ぜひ覚えておきましょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (2018-11-07T00:00:01Z)
¥5,720 (コレクター商品)