どうも、木村(@kimu3_slime)です。
大学で線形代数学を学ぶためには、どんな中学・高校数学の単元を身に着けている必要があるのでしょうか。
今回は、数学概念の相互関係を、初等代数・幾何・論理のスキルツリーとしてひとつの図にまとめてみました。全体像や論理構造、単元一覧を掴んだり、ロードマップとして活用してみてください。
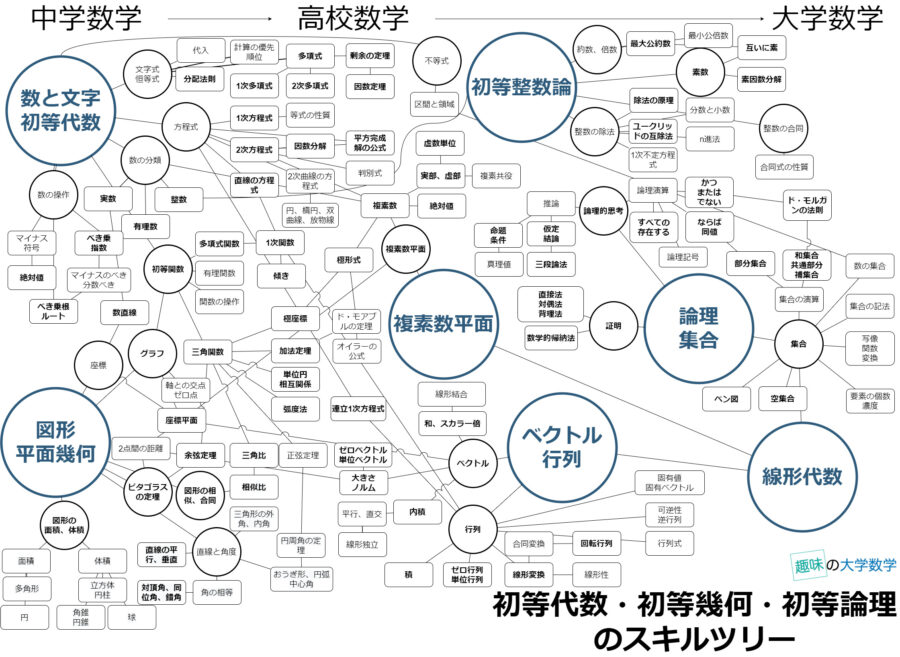
情報量が大きいので、画像を拡大してみるか、PDFバージョンでご覧ください。
重要なキーワード
僕の主観にもとづいて、重要で身につけておいてほしいキーワードをまとめておきます。
数と文字、初等代数
- 分配法則
- 多項式
- 1次多項式
- 2次多項式
- 剰余の定理、因数定理
- 方程式
- 1次方程式
- 2次方程式
- 因数分解
- 平方完成、解の公式
- 直線の方程式
- 数の分類
- 整数
- 有理数
- 実数
- 複素数
- 絶対値
- べき乗、指数
- べき乗根、ルート
図形、平面幾何
- 座標
- 数直線
- 座標平面
- グラフ
- 多項式関数
- 1次関数、傾き
- 図形の面積、体積
- 直線の平行、垂直
- 対頂角、同位角、錯角
- 図形の相似、合同
- 相似比
- ピタゴラスの定理
- 三角関数
- 三角比
- 単位円、相互関係
- 余弦定理
- 加法定理
- 極座標
- 弧度法
初等整数論
- 約数、倍数
- 最大公約数
- 互いに素
- 素数
- 素因数分解
- 除法の原理
- ユークリッドの互除法
- 合同式
偶数+奇数はいつでも奇数? 読み解き方、よくある間違いと証明
論理、集合
- 推論
- 仮定、結論
- 命題、条件
- 三段論法
- 論理演算
- かつ、または、でない
- ならば、同値
- すべての、存在する
- ド・モルガンの法則
- 証明
- 直接法、対偶法、背理法
- 数学的帰納法
- 集合演算
- 和集合、共通部分、補集合
- 部分集合
- 空集合
- ベン図
「AならばB」のよくある誤解から学ぶ、論理学入門(対偶、逆、否定、真偽表)
記号論理、命題論理入門:覚えるべき論理記号(否定、かつ、または、ならば、同値)とは
論理に関するド・モルガンの法則を真偽値の計算(プログラミング)で確かめる
ベクトル、行列、線形代数
- ベクトル
- 和、スカラー倍
- 大きさ、ノルム
- ゼロベクトル、単位ベクトル
- 内積
- 行列
- 積
- ゼロ行列、単位行列
- 連立一次方程式
- 線形変換(一次変換)
- 回転行列
1次方程式を行列で解くメリット・方法・条件について、幾何学的に見る
線形代数学の応用:CG・画像処理(拡大縮小・反転、回転、せん断)について
複素数平面
- 複素数
- 実部、虚部
- 虚数単位
- 絶対値
- 実部、虚部
- 複素数平面
- 極形式
- オイラーの公式
以上で挙げたキーワードを身に着けていれば、大学初年度の線形代数の教科書を読めるようになるでしょう。
中学高校数学のやり直しなら:高校数学のやり直し・独学のやり方、おすすめ教材、高校数学のやり直し・独学のやり方、おすすめ教材
大学数学に入門、予習したいなら:大学入学前に数学を予習したい人におすすめの本・勉強法
木村すらいむ(@kimu3_slime)でした。ではでは。
中高一貫教育をサポートする体系数学〈4〉高校2年生用 微積分の基礎と数列・ベクトル
数研出版 (2018-01-01T00:00:01Z)
¥4,406 (コレクター商品)
中高一貫教育をサポートする体系数学5複素数平面と微積分の応用
数研出版 (2019-01-25T00:00:01Z)
¥4,656 (コレクター商品)
岩波書店 (2019-05-25T00:00:01Z)
¥5,763 (コレクター商品)
岩波書店 (2019-05-25T00:00:01Z)
¥2,640
岩波書店 (2019-05-25T00:00:01Z)
¥2,640
岩波書店 (2019-05-25T00:00:01Z)
¥6,685 (コレクター商品)
岩波書店 (2019-05-25T00:00:01Z)
¥6,158 (コレクター商品)
こちらもおすすめ
微積分・初等解析のスキルツリー:必要な中学・高校レベルの数学