どうも、木村(@kimu3_slime)です。
サインやコサインなどの三角関数のグラフを描けるようになることは、高校数学で求められる能力です。一体なぜそんなグラフを描く練習をするのでしょうか? 三角関数は波や振動など、周期的な現象を表すために使われ、無機質な「数学」におさまらない重要さを持っています。
今回は、音の波を例に、三角関数のグラフが持つ意味やイメージを紹介し、それをもとに三角関数のグラフの書き方を紹介します。
前提として、三角関数の特殊なケースでの値や、ラジアンを使った角度の表し方(弧度法)は知っているものとします。
三角関数のグラフの意味
僕たちが聞いている音というものは、空気の振動を耳(鼓膜)で読み取ったものです。
音は目には見えないものの、一種の波(音波)です。音の波形はコンピュータ上で見ることができますので、ぜひ見てみてください。
音の主な構成要素としては、大きさと高さの2つがあります。
(本当は音色という要素があるのですが、今回は簡単のため、三角関数による波:サイン波という単純な音しか扱いません。まずは単純な音色をどう捉えるかを学びましょう。)
振幅:音の大きさ
スマホやパソコンでは、音量ボタンによって音量を上げたり下げたりすることができます。上の動画では、波の縦幅は一定であり、音の高さは変わりながらも、音量が一定でした。音量は、三角関数のグラフで言えば波の幅広さ:振幅に対応しています。
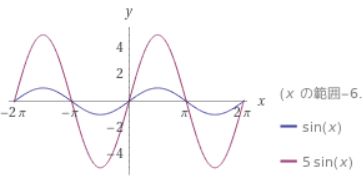
次に図示したのは、\( \sin x \)と\(5 \sin x\)のグラフです。
画像引用:WolframAlpha
振れ幅が0になるタイミングは変わりませんが、波の大きさが5倍になっています。音量を上げるとはこの縦幅を伸ばすことで、音量を下げるとはこの縦幅を縮めることです。
数学的には、サインの取りうる値は\(-1 \leq \sin x \leq 1\)です。一方で、その5倍した関数は\(-5 \leq 5\sin x \leq 5\)と最大値・最小値が5倍になっています。
一般に、三角関数\(A \sin x\)にかかっている正の定数\(A\)を、その関数の振幅(amplitude)と呼びます。振幅の大きさは、光で言えば明るさですし、水の波で言えば波の大きさです。\(\sin x, 2 \sin x ,3\sin x ,\dots\)のグラフを頭の中で描いて、強弱をイメージしてみてください。
音の大きさを表すためによく使われる単位として、デシベル(dB)があります。人間が音のスケールを捉えやすくするために対数を用いた単位です。
参考:騒音の基礎知識
周期と周波数:音の高さ
冒頭の動画では、音がだんだんと高くなってゆき、それに合わせて波が素早く振動するようになりました。
音の高さに対応するのが、三角関数の周期と周波数です。ゆっくりと振動する波を低い音、素早く振動する波を高い音として、僕たちは聞き分けています。
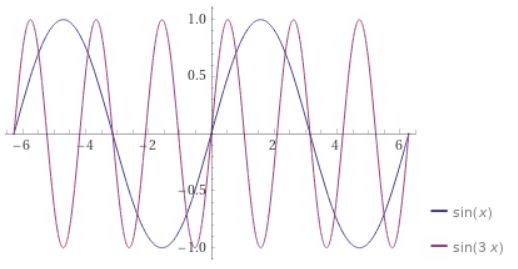
数学的には、三角関数\(\sin x\)の中身の部分の変化率に対応しています。\(\sin x, \sin 3x\)のグラフを見てみましょう。
画像引用:WolframAlpha
見比べてみると、どちらも振幅は同じです。つまり、\(-1 \leq \sin x \leq 1\)、\(-1 \leq \sin 3x \leq 1\)という関係性は変わりません。グラフを書くときも、縦の幅は同じです。
異なるのは、ひとつの波の横幅です。音で言えば、素早く振動している\(\sin 3x\)の方が\(\sin x\)より高く聞こえます。
この横幅を捉えるために、2つの見方:周期と周波数があります。
数学的にわかりやすいのが、周期です。三角関数では\(\sin x = \sin (x+2\pi)\)という式が常に成り立ち、これは三角関数の周期性と呼ばれます。このとき、\(\sin x\)の周期は\(2 \pi \)であると言います。\(0 \leq x \leq 2 \pi\)でのグラフの形を覚えてしまえば、あとは\(2\pi \leq x \leq 4 \pi \)でも\(-2\pi \leq x \leq 0 \)でも形は同じなのです。
一般に、\(f(x)=f(x+T)\)を常に成り立たせる最小の定数\(T>0\)を、関数\(f\)の(基本)周期と呼びます。
(例えば、\(\sin x = \sin (x+4\pi)\)も成り立つので、三角関数の周期は\(4\pi\)でもあると言えます。\(T\)が周期であるとき、\(2T,3T,4T,\dots\)も周期になります。ただし、単に周期という言葉を使うときは、周期のうち最小のもの:基本周期を普通は意味するので注意しましょう。)
\(\sin 3x\)の周期を求めてみましょう。イメージがわかないときは、\(x\)に具体的な値を入れて、グラフを描いてみると良いと思います。例えば、\(x=2\pi \)のとき、\(\sin 3x =\sin 6\pi =0\)です。
\(\sin x\)は\(x=2\pi\)で一周します。\(\sin 3x\)が最初に一周するとき、\(3x = 2\pi \)となりますが、つまりこれは\(x = \frac{2\pi}{3} \)に対応します。これが周期ではないかと検討すると、\(\sin (3(x+ \frac{2\pi}{3} ))= \sin (3x +2\pi)= \sin 3x\)が成り立つので、\(T= \frac{2\pi}{3} \)が周期であると言えました。
まとめると、\(\sin x\)の周期は\(2\pi\)で、\(\sin 3x\)の周期は\(\frac{2\pi}{3}\)です。中身の部分が3倍となることで、周期は\(\frac{1}{3}\)倍に短くなっていることに注意しましょう。一般に、\(\sin kx \)の周期は\(\frac{2\pi}{k}\)となります(確かめてみてください)。
三角関数が一周するのにかかる時間が周期であるということですが、周期の逆数を周波数(frequency)、または振動数と呼びます。
\[ \begin{aligned}F = \frac{1}{2\pi }\end{aligned} \]
例えば、\(\sin x\)の周波数は\(\frac{1}{2\pi}\)、\(\sin 3x\)の周波数は\(\frac{3}{2\pi}\)です。周波数は、一定の時間あたりに何回波が振動するかを表しています。\(\sin 3x\)は\(\sin x\)の3倍のペースで振動していることが、周波数の立場からするとわかりやすくなっていますね。
周波数の単位には、ヘルツ(Hz)が用いられます。楽器で用いるドレミファソラシドの音は、次のような振動数に対応したものです。
1オクターブの振動数 音 ド レ ミ ファ ソ ラ シ ド 振動数(Hz) 261 293 329 349 392 440 493 523
引用:楽器の長さと基本振動数
低いドと高いドの音の差は1オクターブと呼ばれますが、1オクターブの違いは周波数が2倍(高い方から見れば半分)になることにあります。ちょうど2倍(半分)の関係の音が、人間の耳には似た音(高さは違うけどドの音)と聞こえるのは、不思議ですね。
周期や周波数は、音で言えば高さ・低さに対応していますが、光で言えばその色合いに対応しています。人間は周波数の低い電磁波を赤色の光に、周波数の高い電磁波を青色の光として見ているわけです。
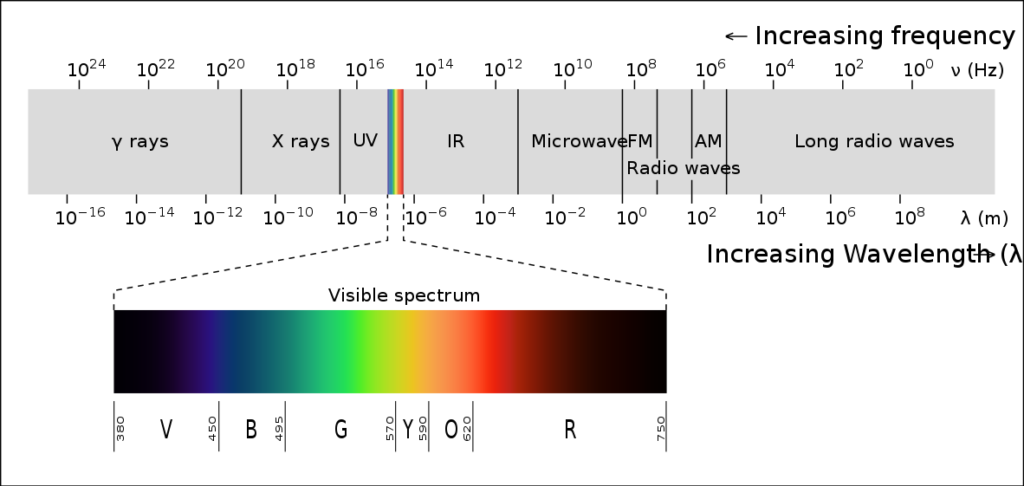
画像引用:File:EM spectrum.svg – Wikimedia commons
位相:音を聞き始めるタイミング
音の特徴は大きさと高さ、つまり振幅と周期(周波数)であるという話をしました。三角関数のグラフの形は、この2つさえあれば決まっています。
しかし細かいことを言えば、波のどの部分から書き始めるか、音をどの部分から聞き始めるか、という問題があります。それを捉えるのが、初期位相です。
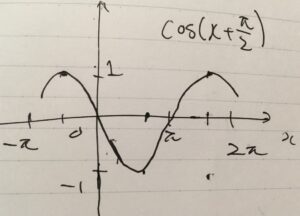
\(\sin x\)と\(\sin (x -\frac{\pi}{2})\)のグラフを図示しました。
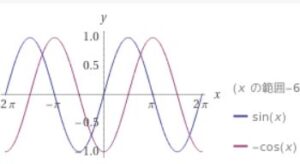
画像引用:WolframAlpha
\(\sin (x -\frac{\pi}{2})\)は、\(\sin x\)の\(x\)を\(x-\frac{\pi}{2}\)に置き換えたもの、つまり\(x\)軸方向に\(\frac{\pi}{2}\)だけ平行移動させたものです。\(x =0\)のときの角度\(-\frac{\pi}{2}\)を、\(\sin (x -\frac{\pi}{2})\)の初期位相(initial phase)と呼びます。
一般には、\(A \sin (k(x + \alpha))\)における\(\alpha\)が初期位相です。\(\sin x =\sin (x+0)\)であり、初期位相\(0\)であると言えます。
コサインとサインの関係として、\(\cos x = \sin (x+\frac{\pi}{2})\)という関係があり、コサインはサインから位相が\(\frac{\pi}{2}\)だけ遅れた関数と見れます。コサインのグラフを描けという問題も、結局この関係式からサインのグラフに帰着されるものです。
振幅と周期(周波数)が特定され、三角関数の形がわかったら、原点\(x=0\)でどの段階(位相)から始めるかに注意しましょう。
三角関数のグラフの書き方
今まで考えてきたことをもとに、三角関数のグラフの書き方を紹介します。
\(f(x) =-3 \cos (\frac{x}{4} + \frac{\pi}{8})\)のグラフを描きたいとしましょう。注目すべきポイントは、振幅は何か、周期(周波数)は何か、初期位相は何かということでした。音の大きさ、高さ、聞き始める位置によってひとつの音は決まるのです。
今までの議論をまとめると、三角関数は\(A \cos (k (x +\alpha))\)という形に一般的に表されます。
振幅は\(A=-3\)ですね。周期は\(\frac{x}{4} =2\pi \)となる\(x\)なので、\(T = 2\pi\)です。そして初期位相は\(\cos (\frac{x}{4} + \frac{\pi}{8})\)を見れば、\(\frac{\pi}{8}\)だ……と考えないように注意しましょう。\(f(x) = -3 \cos (\frac{1}{4} (x + \frac{\pi}{2}))\)なので、初期位相は\(\alpha = \frac{\pi}{2}\)です。基準を\(\frac{x}{4}\)に揃えましょう。
これらの情報をもとに、グラフを描いていきます。
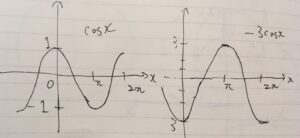
いきなりだと難しいので、分解して考えましょう。基本は、まずコサイン\(\cos x\)のグラフをイメージします。そしてそれを少し変形した、\(f_1(x) =-3 \cos x\)、\(f_2(x) = \cos (\frac{x}{4})\)、\(f_3(x) =\cos (x +\frac{\pi}{2})\)のそれぞれのグラフをまず描いてみましょう。
\(-\cos x\)は、\(\cos x\)のグラフを上下反転させたもの、\(x\)軸について対称な形をしています。それを3倍したグラフが、\(-3\cos x\)です。
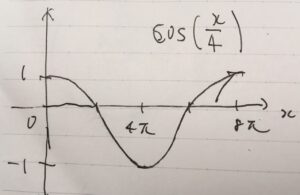
\(\cos (\frac{x}{4})\)は、さきほどの議論により周期が\(8\pi \)です。まず横幅として\(8\pi\)を取り、中間地点として\(4\pi\)に注意して、コサインのグラフを描けば良いです。
\(\cos (x+\frac{\pi}{2})\)は、\(x= -\frac{\pi}{2}\)が\(\cos x\)でいう\(x=0\)に対応するので、\(\cos x\)のグラフを左側に\(\frac{\pi}{2}\)だけ動かしたものになります。
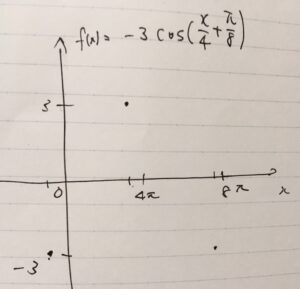
以上のグラフを参考に、\(f(x) =-3 \cos (\frac{x}{4} + \frac{\pi}{8})\)のグラフを描きましょう。
まず横の幅、すなわち周期は\(8\pi\)だったので、横に直線を描いて目印をつけましょう。半分の\(4\pi\)も目印をつけます。縦の幅、振幅は\(3\)なので、縦軸にもその大きさを記します。
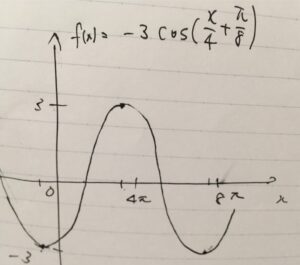
コサインのグラフを描きますが、振幅がマイナスなので、左から順に、谷、山、谷という形になるわけです。頂点に目印を取りました。
頂点の位置は\(0, 4\pi , 8 \pi\)ではなく、初期位相の分だけ全体が横にずれています。つまり、\(\frac{\pi}{2}\)だけ左側に目印を取りましょう。そして、頂点の間をなめらかにつなげば、グラフができあがります。
以上、三角関数のグラフの意味と書き方を、音の波を例に紹介してきました。その特徴を表しているのは、波長:音の大きさ、周期(周波数):音の高さで、聞き始めるタイミングは初期位相と呼ばれます。
音や光、水の波や電気は、三角関数によって表されます。どうして三角関数が登場するかと言うと、それは波動方程式という偏微分方程式を学ぶと理解できるでしょう。また、光や音やコンピュータにおいて電気信号としてやりとりされますが、複雑な波をデジタルに捉えるにあたってはフーリエ解析と呼ばれる理論が役立ちます。
より本質的な理論を学ぶ前段階としても、ぜひ三角関数のイメージ、式とグラフの対応関係をぜひ描けるようになってみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
線形代数の応用:関数の「空間・基底・内積」を使ったフーリエ級数展開
熱方程式の解き方:変数分離法、フーリエ級数展開(1次元、有界領域)