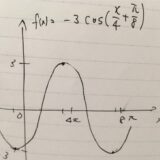
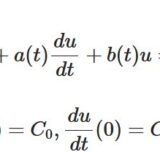どうも、木村(@kimu3_slime)です。
高校~大学数学の最初に、行列というものを学ぶかと思います。行列は単に数を並べたものだけでなく、図形的に捉えることができるものです。
今回は、行列にあまり馴染みのない人向けに、行列が持つ変換としての側面について、点や直線の変換による像の求め方を紹介します。
行列によって点を変換する
今回考えていくのは、\(2 \times 2\)の簡単な行列です。
\[ \begin{aligned}A= \begin{pmatrix} 0.5 & 0 \\ 0 & 2 \end{pmatrix}\end{aligned} \]
行列は、平面\(\mathbb{R}^2\)上の点\(x=(x_1,x_2)\)を、別の点\(Ax\)に対応させています。
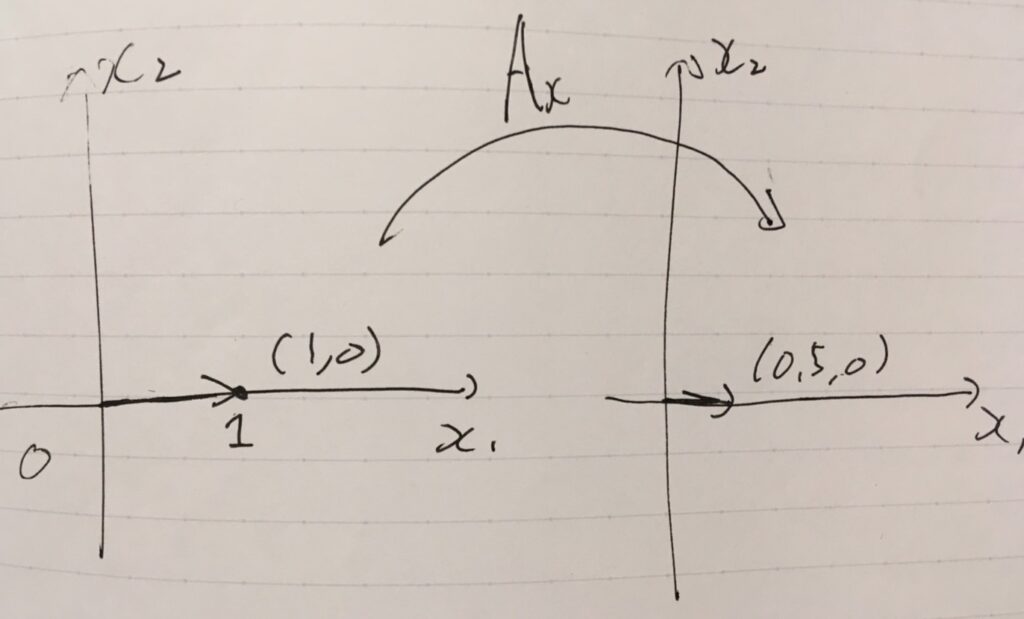
例えば、\((1,0)\)という点(ベクトル)はどこに写るでしょうか。それを考えるためには、その点に行列を左から掛ければ良いです。
\[ \begin{aligned}\begin{pmatrix} 0.5 & 0 \\ 0 & 2 \end{pmatrix} \begin{pmatrix} 1\\0 \end{pmatrix} = \begin{pmatrix} 0.5 \times 1+0\times 0 \\ 0\times 0 + 2 \times 0\end{pmatrix}= \begin{pmatrix} 0.5\\ 0\end{pmatrix}\end{aligned} \]
もともとは\((1,0)\)という点が、別の点\((0.5,0)\)に写りました。\(x_1\)軸方向の大きさが半分になっています。
別の点\((0,1)\)を\(A\)によって変換するとどうなるでしょうか。
\[ \begin{aligned}\begin{pmatrix} 0.5 & 0 \\ 0 & 2 \end{pmatrix} \begin{pmatrix} 0\\1 \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \end{pmatrix}\end{aligned} \]
\((0,1)\)は、\((0,2)\)に写されました。\(x_2\)軸方向に大きさが2倍になっていますね。
具体的な点ではなく、一般に文字で表した点\(x=(x_1,x_2)\)は\(A\)によってどこへ写るでしょうか。
\[ \begin{aligned}\begin{pmatrix} 0.5 & 0 \\ 0 & 2 \end{pmatrix} \begin{pmatrix} x_1\\x_2 \end{pmatrix} = \begin{pmatrix} 0.5 x_1 \\ 2 x_2 \end{pmatrix}\end{aligned} \]
確かに、\(x_1\)方向に縮めて、\(x_2\)方向に伸ばすような変換であることが見て取れますね。
このように、行列\(A\)を「ベクトル\(x\)を別のベクトル\(Ax\)に対応させる規則」として見るとき、行列は一次変換、または線形変換(linear transformation)と呼ばれます。
上で扱った行列によって画像を変換してみると、次のようになります。


コンピューターにおける画像処理、CGを考えるときには、行列によって表せる一次変換・線形変換の考え方が役立つでしょう。
参考:線形代数学の応用:CG・画像処理(拡大縮小・反転、回転、せん断)について
直線の像の求め方
ここまではひとつの点が行列によってどう写されるかを見てきましたが、点の集まり、特に直線がどう写されるかを考えることもできます。
\[ \begin{aligned}A= \begin{pmatrix} 0.5 & 0 \\ 0 & 2 \end{pmatrix}\end{aligned} \]
によって\(x_2 = 2 x_1 -1\)という直線はどんな図形に写されるでしょうか。(\(x_1,x_2\)という記号がイメージしにくかったら、\(x,y\)を使って\(y= 2x -1\)がどう写されるか、と考えても良いです。)
求めたいのは、直線上の一般的な点\(x\)が、\(A\)によって写る先\(Ax\)です。
つまり、写す前の点、まず直線上の点を一般的に表す必要があります。それを\(x=(x_1,x_2)\)としましょう。直線上の点は\(x_2 = 2 x_1 -1\)という条件を満たすので、\(x= (x_1,2x_1 -1)\)と表せますね。
したがって、
\[ \begin{aligned} Ax &=\begin{pmatrix} 0.5 & 0 \\ 0 & 2 \end{pmatrix} \begin{pmatrix}x_1 \\ 2x_1 -1\end{pmatrix} \\ &=\begin{pmatrix}0.5 x_1 \\ 4x_1 -2 \end{pmatrix} \end{aligned} \]
という点たちに写ることがわかりました。\(x_1\)に具体的な数値を入れて動かすと、どんな形になっているか想像できるでしょうか。直線ですね。
この結果を、直線の方程式の形にしましょう。\(Ax\)の第一成分を\(0.5 x_1 =y_1\)と置けば、第二成分は\(y_2= 4x_1 -2 = 8y_1 -2\)と表されます。すなわち、\(y_2 = 8y_1 -2 \)という直線が得られました。
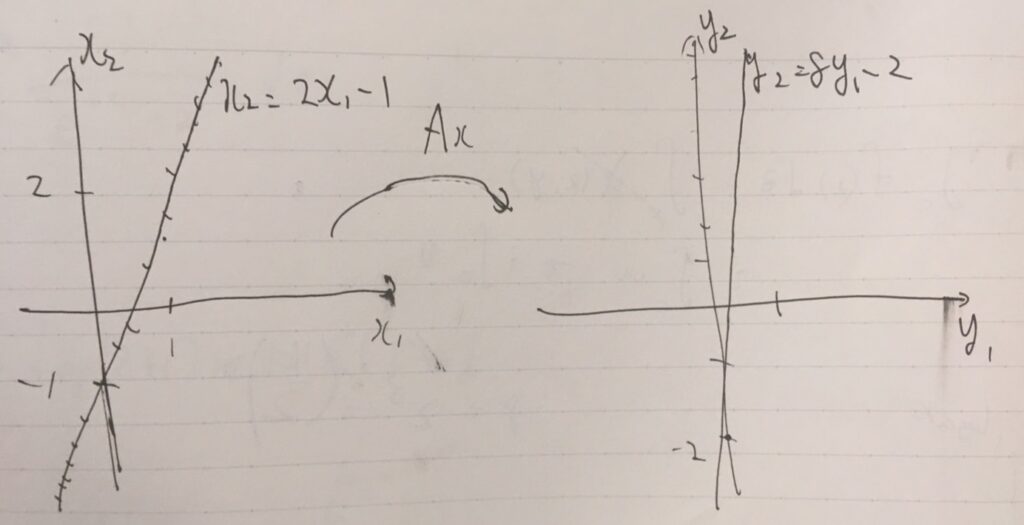
つまり、\(x_2 = 2 x_1 -1\)という直線は、\(A\)によって\(y_2 = 8y_1 -2 \)という直線に写されています。傾きが4倍になり、かなり縦に伸びていますね。
一般に、行列によって直線を写すと、その像も必ず直線になります。直線を直線に写すような変換だから、線形変換と呼ばれるわけですね。
以上、行列によって点や直線を写すとどうなるか、一次変換・線形変換の考え方を紹介してきました。
直線の像の求め方がわからないならば、まずは具体的な点がどう写るか実験してみると良いと思います。それができたら、一般の点がどう写るか。それができたら、直線上の点を一般的に表して、それがどう写るかを考えれば良いです。
行列とベクトルの積の定義・計算方法を復習しながら、行列により定まる変換の幾何学的イメージをつかみましょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
線形代数学の応用:CG・画像処理(拡大縮小・反転、回転、せん断)について