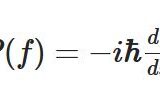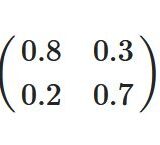どうも、木村(@kimu3_slime)です。
当サイト「趣味の大学数学」では、大学数学の基礎として微積分と線形代数をできるだけ多くの人が気軽に学べるようになったらいいな、と思っています。
多くの人にとって、それを学ぶためには、小学校・中学校・高校の算数・数学の復習が必要です。
その内容は「中学・高校数学のロードマップ ~ 分野一覧と学ぶ順序」にまとめましたが、もう少し簡単に学べたら嬉しいですね。
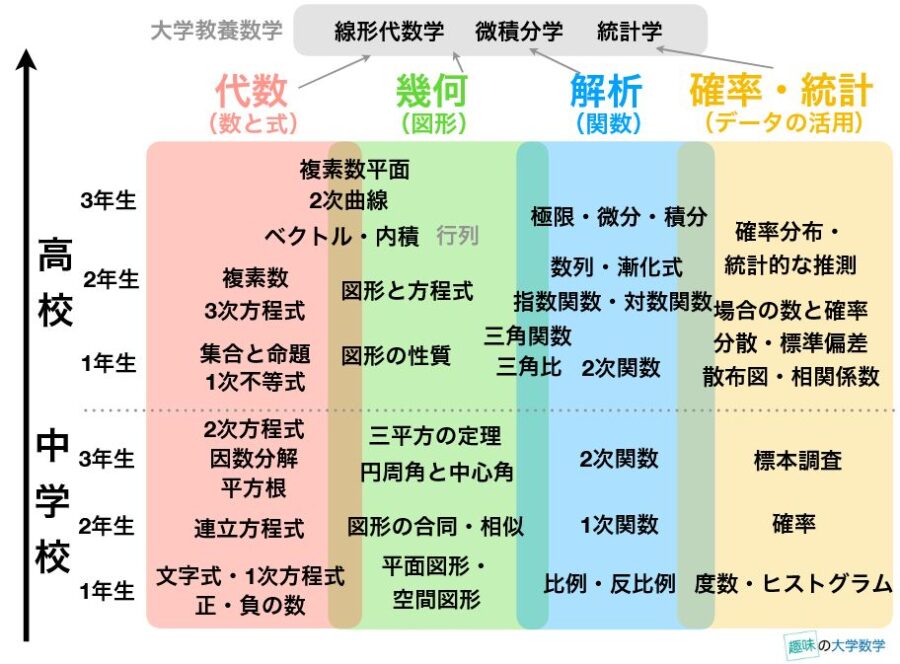
そこで今回は、「最短で学ぶ小中高の数学」という題で、どんな数学が最低限は必要と僕が考えているか、暫定的に紹介します。
目次
最短で学ぶ小中高の数学
おおざっぱには、僕は次のようにまとめます。
- 小学校:2,3桁程度の自然数・分数・整数の四則演算
- 中学校:初等代数(1・2次の多項式、方程式・平方根・不等式、座標平面・関数、面積、ピタゴラスの定理)
- 高校:初等関数(指数・対数・三角関数)と微積分
- 高校:ベクトルと行列
学校のカリキュラムで含まれやすい、平面幾何(図形)、確率・統計、整数論、集合・論理、数列、複素数平面について削っています。
僕は本当は、理屈を知った上で数学を学ぶほうが楽しいと考えています。一方で、理屈を知らなくてもきちんと計算できれば使えるのが数学の良いところでもあります。
最低限の計算能力を身につければ、後で理屈や基礎はフォローすることができると思いますので、まずはこれらのトピックの内容を知って確実に計算できるのが大事だと考えています。
では、上記のトピックで具体的にどんな内容を想定しているか、ざっくりと見ていきましょう。
小学校:四則演算
算数の計算が、1.確実に 2.素早く できることは、数学の基礎体力となります。
中学校以降の数学では、数の代わりに記号も使いますが、結局は普通の数の簡単な計算をたくさんします。簡単な問題に帰着させるのが数学の理論の仕事で、その簡単な計算問題を解く腕力は必要です。
足し算・引き算と10進法
3以上の数を文字を使わずに扱うのは、人間には難しいです。そこで編み出されたのが、10進法をベースにした計算法です。
繰り上がりの計算のようすを見るだけで、その人が算数が得意か苦手か、ある程度判別できるような気がします。
例えば、\(8+7\)をどう計算するでしょうか。\(5+3+5+2 = 10+5\)としても良いし、\(10-2+10-3=20-5\)としても良いでしょう。10を作り出す工夫によって、足し算の不安は減るでしょう。
引き算は、足し算を逆にした問題です。\(19-8\)を計算したいなら、\(8\)にいくつ足せば\(19\)になるか、と考えれば良いです。最初のうちは\(5\)じゃ足りない、\(12\)じゃ足しすぎ、といったように試行錯誤をすることになるでしょう。一発で答えを出すことにこだわらず、推測する訓練をしていれば、やがてスムーズにできるようになります。
掛け算・指数
いわゆる掛け算九九を覚え、その後筆算をする教育が主流です。とりあえず覚えるのも悪くはないのですが、まずは掛け算の定義(意味)を知っておくのが大事だと思います。
\[ \begin{aligned}2\times 3 =2 +2+2\end{aligned} \]
といったことです。別に\(2\times 3 =3+3\)としても良いですが。この話を知っていれば、掛け算の問題は足し算の問題に戻すことができます。
\(7\times 9\)の値は何か、九九の暗記を忘れても、理屈を知っていれば計算できます。例えば、\(7\times 10 =70\)だから、\(7 \times 9=70-7=63\)といったように。
ここでは、\(7 \times 9 =7 \times(10-1)= 7 \times 10 -7 \times 1\)という分配法則が成り立っています。足し算と掛け算を結びつける分配法則は、掛け算の計算を楽にしてくれます(それが筆算の原理です)。カッコの意味と使い方はここで身につけます。掛け算は難しいかもしれませんが、うまく計算できる方法を考えてみましょう。
参考:6÷2(1+2) の答えは9?1? 出題者はカッコを使うべき、カッコの前のマイナスの外し方:分配法則を理解する、自然数の掛け算の交換法則が成り立つのはなぜか:定義と証明
同じ数をいくつも掛け算する計算は、数学でよく使います。\(2^3 = 2\times 2 \times 2\)と右上にかける回数を書き、これを2の3乗(一般にべき乗)と呼びます。かける回数のことを指数と呼びますが、指数を見ることによって大きな数や小さな数をわかりやすく表現できます。
割り算・分数・小数
小学校で学ぶ割り算には、あまりを考える割り算とあまりを考えない割り算があり、初めて学ぶときには混乱しやすいです。数学では後者を使う機会の方が多いので、最短コースではあまりを考えない割り算だけ学べば良いと思います。
割り算・分数は、あるもの(分子)を別のもの(分母)を基準にして分けることです。
加減乗に比べて、「等しく分ける」操作は感覚的に処理しづらく、結構難しいようです。それもそのはず、自然数の加減乗の結果は自然数ですが、割り算の結果は一般に分数(有理数)となるからです。分数の正体がよくわからないと考えるのは自然なことで、それは新しい「数」を仲間に入れているからです。
例えば\(1\)という数をいくつかに分割することを想像するのは難しいのかもしれません。導入としては、図形的なこと、長さや面積について感覚的に知っておくと良いでしょう。加減乗の結果をタイル並べに対応させ、そこから逆に割り算がどんな計算か学べます。また、ひもやケーキを分けるとどうなるか、試してみて学ぶことがあるでしょう。
分数同士の掛け算や割り算は、間違いが多く苦手になりやすい分野です。簡単なケースに戻って、計算に納得できるか考えてみましょう。
参考:なぜ分数の割り算はひっくり返してかける? 分数の定義と逆数について
分数の特殊な表し方として、小数があります。小数の正体は10や100を分母とする分数なので、相互に読み替えられると良いでしょう。また、3割引や150%といった比の言葉が、数学的に何を意味しているのか読み取れるようになりましょう。
負の数・整数
マイナスの数は、比較的歴史が浅く、それだけ人間には受け入れ難かった数なのでしょう。中学校で扱いがちですが、基礎的な計算という面では小学校とセットの方がまとまりが良いです。
生活の中で見かけるマイナス、気温やゲームのスコア、数字の相対的な増減などの例をいくつも考えてみると馴染めるかもしれません。
分数と同じように、マイナスの数も新しい数の仲間として考えます。そうした数は整数と呼ばれるものです。
最初は、個別の数\(-5,-\frac{1}{10}\)について、数直線上に図示してみると良いでしょう。その上で、正の数と負の数、負の数と負の数の計算(加減乗除)を学びます。\((-5)\times 3\)という式を見たときに、どこがひとまとまりの数で、何の計算か読み取って処理できることが大事です。
参考:マイナスかけるマイナスはなぜプラスになるのか:分配法則から
中学校:初等代数
ここからがいわゆる「数学」っぽくなります。つまり、\(x\)や\(y\)といった記号が出てきます。この記号を使って考えることを、数学では代数(だいすう)と呼びます。数の代わりに記号を使うわけです。
代数は数学を大きく発展させることになったツールです。高度なことができるようになった分、文字だらけで「数式」っぽくいかめしく感じもするでしょう。中学では、これら代数を怖がらずに扱える能力が求められます。
文字式、変数と代入
まずは、\(x,y\)といった文字を含んだ式、文字式とは何かを学びます。
\(2\times 1,2 \times 2 ,2\times 3\)といった数式は、まとめて\(2 x\)と表せます。ここで右側の数を\(x\)という文字・記号で表しました。このように変化しうる数を記号で表したものを、変数や不定数と言います。
\(2x \)がどんな値を持っているのかは、\(x\)の値が決まらない限りは求められません(わからない)。\(x = 3\)のときの値は、\(2\times 3 =6\)と考えます。これは不定であった文字と具体的な値を置き換える操作で、\(x=3\)という式による置き換えを代入と呼びます。
数学の文章では、何が変数となっているかを読み取るのが大事です。文字式を使うことで、数多くの数式をひとつにまとめること(一般化)ができます。
多項式、恒等式の計算
よく使う文字式には、名前がついています。そのうちもっとも基本的なものが多項式と呼ばれるグループで、単純なものが\(2x+1\)のような1次多項式、\(x^2 +4x\)のような2次多項式です。
多項式は文字を含む式ですが、文字を含んだまま計算(加減乗)することができます。\((x+1)(x+3)=x^2+4x+3\)のような分配法則を使った展開に慣れましょう。
1次多項式の積に具体的な値を代入してみると、左辺と右辺で値が等しくなることがわかるでしょう。「文字のまま扱う」「代入する」2つのフェーズを区別して計算するのが大事です。
方程式と平方根、不等式
\(x+7 =1\)のように、「文字式=文字式」で表される等式において文字\(x\)の値を求める問題を方程式と呼びます。
文字式(恒等式)と方程式は混同されやすいですが、別物です。方程式\(x+7 =2\)においては、\(x\)を未知数と呼びます。
文字式において\(x\)の正体は普通は決まっていないのですが、2つの文字式が等しいと、そこからただひとつの値が決まるケースがあります。例えば、\(x+7 =2\)ならば\(x=-5\)の可能性しかありえません。方程式を成立させる\(x\)の値を、変数\(x\)に関する方程式の解と呼びます。
まずは1次方程式を学び、等号の性質を使って解けることを知るでしょう。1次方程式の解はひとつですが、2次方程式では一般に2つの解を持ちます。2次方程式では因数分解を使えば解けます。
参考:なぜ移項すると符号が変わるのか 方程式・等式の意味を考え直す、因数分解で2次方程式がなぜ解けるか:積が0となる数の性質
2次方程式を解こうとすると、例えば\(x^2 =2\)を考えると、整数や分数の範囲に解がないことに気づくでしょう。そこで導入されるのが、平方根やルートです。
2次方程式には基本的に2つの解(プラスとマイナス)があります。ルート記号は、そのプラスの方を表しているという取り決めに注意しましょう。
参考:平方根とルートの違い:ルート外しの注意点、ルートを含む等式の両辺を2乗するときの注意点:逆も成り立つか
\(\sqrt{2}\)のように有理数として表せない数は、無理数と呼ばれます。無理数もマイナスの数と同じように、歴史的に受け入れられるまでに時間がかかったようです。後に紹介するように、例えば直角三角形の斜辺の長さとして\(\sqrt{2}\)は表れます。
無理数は実用的に表れる数ですが、ルート記号を使わずにシンプルに表現するのが難しいです。そこで近似値を使って計算することがあります。ルートの値を語呂で覚えるのも良いですが、不等式を使って比較してみるとどんな大きさの数なのかわかるでしょう。
参考:ルートの近似値の求め方 不等式を使って大小比較、有理数と分数、無理数の違い:よくある誤解を越えて
不等号は、等号と違って、左辺と右辺の数の大きさに違いがあることを意味するものです。\(x<y\)は\(y\)が\(x\)よりも真に大きいこと、\(x \leq y\)は\(x=y\)または\(x<y\)を意味します。
不等号の意味はよく勘違いしやすいので注意しましょう。
参考:不等式の証明で等号成立を確かめる必要がないのはなぜか:≦の意味
\(2x >5\)のように、「文字式 不等号 文字式」の形の式を不等式と呼びます。方程式では解は1つ、2つ、0個といったものですが、不等式では特定の数が解となるわけではなく、数を示す範囲が解となります。例えばさきほどの不等式ならば、\(x> \frac{5}{2}\)を満たすすべての\(x\)が不等式の解です。解の範囲を数直線で図示してみましょう。
座標平面、関数
ここまでは基本的に1つの変数\(x\)のみを扱うことが多いです。しかし、座標平面や関数の分野では、\(x,y\)という2つの変数を考えます。
まずは、座標平面を書いてみましょう。平面上の点は、\((x,y)=(1,2)\)といったように2つの数の組で表されます。座標\((-3,2)\)がどこなのか、図示してみてください。
「気温が上がると出歩く人が増える」といった関係は、数学では関数として表せます。気温という数を\(x\)、出歩く人の数を\(y\)として、\(y=3x+5\)という式が成り立っているとしましょう。\(x\)に具体的な値を代入し、そのときの\(y\)の値を求め、座標平面に図示してみてください。直線状のグラフができあがるでしょう。一般に、\(x\)の値を決めるとその値\(f(x)\)が決まるような関係\(f\)を、\(x\)を変数とする関数と呼びます。
2つの数の関係性を表す関数の考え方は、数学を科学や現実に応用するために役立つものです。
1次多項式によって表される関数を1次関数、2次多項式によって表される関数を2次関数と呼びます。それらの具体例をたくさん考え、図・座標平面に書いてみてください。その特徴を取り出すために、傾き、軸と頂点、ゼロ点と因数分解といった考え方が役立つことでしょう。
面積、ピタゴラスの定理
長さについては、定規などによって直観的に測れると思って良いでしょう。面積は図形のサイズを数値で表したものです。
1辺の長さが\(a\)、もう1辺の長さが\(b\)の長方形を\(S= a b\)と数値化しましょう、というのが基本です。平行四辺形の面積も長方形と等しい(等積変形)と直観的には認めて良いでしょう。それがわかれば、三角形の面積がその半分\(\frac{1}{2}a h\)であることはすぐにわかります。直角や並行の概念もここで少し学びましょう。
円の面積、立体の体積については、この時点では理屈的に納得しづらいので(積分)、省略して良いかなと思います。平行四辺形と三角形がわかれば最低限足ります。
続いて重要なのが、ピタゴラスの定理(三平方の定理)\(a^2+b^2=c^2\)です。\(a=b=1\)(かつ\(c >0\))のとき、\(\sqrt{2}\)が登場することがわかりますね。
ピタゴラスの定理は、座標平面(やより高次元の対象)における長さを考えるときの基本となっています。例えば三角関数について学ぶときにピタゴラスの定理は欠かせないので、きちんと扱えるようにしましょう。
高校:初等関数と微積分
小中高の数学のひとつの目標点が、微積分です。おおざっぱにいえば、関数の変化と総和を考えます。
高校の微積分が対象としているのは初等関数と呼ばれるもので、初等関数を知るだけでさまざまな現象を表現できます。
ここで初等関数と呼んでいるのは、多項式関数、指数関数・対数関数、三角関数です。
多項式関数
中学では1次関数や2次関数を考えましたが、3次関数、n次関数を考えることができます。これらの総称が多項式関数です。
微積分で何を言っているのかわからなくなったら、まずは多項式関数のケースを考えると話が簡単になるでしょう。
多項式の枠組みを少し外れますが、\(1/(x-1)(x-2)\)のように、多項式割る多項式で定義される関数(有理関数)の簡単なケースも扱えると良いでしょう。
多項式関数では指数を自然数に限定しますが、指数が分数やマイナスのケース、\(\sqrt{x}\)や\(x^{-2}\)のような関数も考えられます(べき関数)。さらに指数関数と対数関数を使うと、\(f(x) =x ^p\)、\(p\)は実数といった関数を一般に考えることができます。
指数関数・対数関数
\(f(x)=x^2\)と\(f(x)=2 ^x\)について比較してみましょう。グラフを書いてみるとわかりますが、後者は倍々ゲームのように圧倒的に早く増えていきます。\(a^x\)の形の関数を、指数関数と呼びます。
多項式関数\(x^2\)では指数\(2\)が一定ですが、指数関数では\(2^x\)と指数が変化するようになっています。式の見た目は似ていますが、全くの別物です。
最初のうちは、\(x=1,2,3\)と自然数を代入してグラフを書くと簡単です。ただし、グラフとして書く以上はその「間」の点もつながっていてほしいです。そこで指数の計算について成り立つ法則:指数法則を取り出して、分数乗やマイナス乗、ゼロ乗といったべき乗も考えられるようにします。
参考:2分の1乗、分数乗とは:指数法則を知ろう、マイナス乗、ゼロ乗とは:指数法則を知ろう
倍々ゲームのように爆発的に増える現象は自然界でもよくあって、それは指数関数的な増加やマルサスの法則と呼ばれています。感染症の拡大も、部分的にはそうですね……。
参考:人類は必ず食糧問題に直面する? マルサスの法則と微分方程式、数学とコロナ~感染症の数理モデルをやさしく解説
指数関数のグラフを書いてみるとわかりますが、あまりに爆発的に増大するので、大きな数同士の違いを読み取るのは難しくなります。
そこで役立つのが対数という考え方です。\(10^2,10^4,10^6\)と増えていく現象ならば、その指数\(2,4,6\)だけ見れば変化の具合がわかりやすいですね。ある数が\(10\)の何乗かと考えるやり方は、常用対数と呼ばれています。地震の規模(マグニチュード)や音の大きさ(デシベル)は対数を利用して測っています。歴史的には、対数は大きな数の掛け算を単純化するために生み出されました。
対数関数は、指数関数の逆として定義されます。\(\log _{10}100 =2\)をどう考えれば良いかというと、\(10^2 =100\)という指数の関係式に戻れば良いのです。逆の考え方は慣れるまで難しいですが、対数の話は指数の話に戻せれば確実です。
三角関数
サイン\(\sin x\)、コサイン\(\cos x\)、タンジェント\(\tan x\)。何の役に立つの、と言われやすい分野です。
これは三角関数という名前や、細切れに教えられやすいのが問題点だと思っています。
まずは理屈抜きにして、三角関数のグラフを見てみると良いと思います。それは波や振動を表しています。一定の周期で繰り返す現象というのは自然界によくあって、それを表すのに便利なのが三角関数というわけです。例えばスマホ、原理としての電気や通信には波を使っていて、三角関数が役立っています。
三角関数は円関数とも呼ばれますが、三角形と円の対応関係が大事です。
参考:サイン、コサインは何の役に立つ? バネの振動と三角関数、三角関数のグラフの意味・書き方:音の波を例に
三角関数の値を一般に求めることは簡単ではありません。そこで、角度が\(\theta = 0,30^\circ,45^\circ,60^\circ,90^\circ\)という特殊なケースの値だけ覚えることになるでしょう。単位円と三角形を書き、ピタゴラスの定理を意識しながら数値とイメージを対応させていきましょう。
鋭角のケースの性質がわかれば、三角関数の種々の性質を使って一般角のケースを考えられます。三角関数の計算は多項式や指数・対数関数の計算に比べると難しいかもしれませんが、加法定理やその派生を扱えるのが大事です。
微分の意味と計算法則
微積分は、歴史的には物体の運動の分析(力学)を通じて発見されました。速度、時間、位置を数式で表すとどうなるか、考えてみるとイメージしやすいです。
微積分は、微分方程式(びぶんほうていしき)の基礎です。それはさまざまな現象を説明できる重要なツールで、これを学ぶために中学・高校数学を学ぶといっても過言ではないと思っています。物理や化学・生物学、その応用としての工業、(近代)科学を大きく押し進めるきっかけとなったのが微積分です。

参考:なぜ中学・高校数学を学ぶのか 数理モデルとしての微分方程式
1次関数は、傾き・変化の割合が一定の関数と言えます。2次関数や他の初等関数は、変化の割合が場所によって変化していますね。そうした各時点での瞬間的な変化の割合を取り出すのが微分です。極限の意味を理解するのは難しいかもしれませんが、2次関数を例にして変化率の式を計算してみるとわかってくると思います。
初等関数の微分の計算は、簡単です。
\[ \begin{aligned}\frac{d}{dx} x^p = p x^{p-1}\end{aligned} \]
\[ \begin{aligned}\frac{d}{dx} e^x =e^x\end{aligned} \]
\[ \begin{aligned}\frac{d}{dx} \log_e x= \frac{1}{x}\end{aligned} \]
\[ \begin{aligned}\frac{d}{dx} \sin x = \cos x\end{aligned} \]
\[ \begin{aligned}\frac{d}{dx} \cos x = -\sin x\end{aligned} \]
こうした関係式が基本です。どうしてこうなるかの理屈はともかく、グラフを書いてみると確かに傾きに対応していることがわかるかと思います。
これらの式はかなりシンプルになっていますが、指数・対数関数では\(e\)という数を、三角関数では角度を\(\pi\)という数を使って表しているおかげです。\(e,\pi\)は分数として表せませんが数学における基本的な定数なので、この機会に扱いに慣れましょう。
参考:なぜe(オイラー数)を学ぶ? 指数関数、対数関数の微分を単純化、ラジアン(弧度法)を学ぶのはなぜ? 三角関数の微分を単純化
微分の線形性、関数の積の微分、合成関数の微分に関する法則を身につけると、初等関数を組み合わせてできる関数の微分も計算できるようになります。
極値・最大値・最小値
微分の考え方を使うと、関数の極値、最大値や最小値が求められます。
グラフと微分関数の関係:増減表を書くことで、関数の形を理解するために微分が役立つことが感じられるでしょう。
積分の意味と計算
中学校で長方形や三角形の面積について学びました。積分を使うと、関数のグラフによって表されるより複雑な図形の面積を求めることができます。
その考え方の基本は、図形を細かい長方形に分けて測るということです。極限の話はわからなくて良いので、図形を長方形で挟み込む近似計算は一度はやってみましょう。
このように積分は関数のグラフのなす面積として定義される量ですが、驚くべきことに、それは関数の微分と大きく関係しています。それが微積分学の基本定理です。
\[ \begin{aligned}\int _a ^b f^{\prime}(x) dx =f(b)-f(a)\end{aligned} \]
もし関数\(f\)の積分\(\int f(x)dx\)を求めたかったら、微分して\(f\)になるような関数\(F\)(原始関数)を見つければ良いということになります。さきほどの微分の公式から、「逆」の関係を読み取れば良いわけです。
こうした微分と積分の関係性があるので、この分野は微積分学とセットで呼ばれ、先に微分を学ぶ(なぜなら積分は微分を使って計算できる)ことになっているわけです。
微分の計算法則があったように、積分にもいくつか計算法則があります。積分の線形性、積の微分に対応する部分積分、合成関数の微分に対応する置換積分です。これらを身につけると、少し複雑な形の初等関数の積分が計算できるようになります。
面積や体積の計算
積分を使えば、さまざまな平面図形の面積、また空間図形(立体)の体積を求めることができます。
現行の数学のカリキュラムでは、円の面積・円周、球の体積・表面積の公式を、理屈がよくわからないまま公式として学ぶことでしょう。それは積分の計算によって導くことができます。
面積や体積は積分で表されることから、逆に一方の公式はもう一方を微分したものになっている……といった関係性にも納得がいくでしょう。
参考:円の面積・円周、球の体積・表面積の公式の覚え方(微積分)
高校:ベクトルと行列
ベクトルと行列は、大学数学の線形代数学の基礎的な部分です。
線形代数学は、CG・画像処理といった図形の変換、ウェブページのランキング化など、コンピュータに関する分野に幅広い応用を持っています(もちろん、コンピュータに限らず数学そのものの基礎となっています)。
参考:線形代数学の応用:CG・画像処理(拡大縮小・反転、回転、せん断)について、なぜ線形代数を学ぶ? Googleのページランクに使われている固有値・固有ベクトルの考え方
ベクトル
座標平面の分野では、点を\((4,3)\)といったように表しました。この数の組をもっと増やすと、\((5,3,2)\)といったように空間上の点を表せます。図形的なイメージから離れて、例えば4人の身長のデータを\(x=(150,160,155,170)\)と4つの数の組で表せます。
このように、いくつかの(たくさんの)数の組をまとめて表せるのがベクトルです。ベクトルは原点からの矢印(有向線分)として見ることもできますが、実際は数ベクトルとして成分計算するのがわかりやすいでしょう。ベクトルの和、スカラー倍といった計算が基本です。
ベクトルは多次元的な量であり、単純に各成分の積を取ったベクトルを考えても応用的な意味が少ないです。しかし、成分の積を足し合わせたものは内積と呼ばれ、それは幾何学的にはベクトルのなす角と関係してきます。
ベクトルの大きさ(長さ)は、各成分を2乗した和のルートとして定義されます。これはピタゴラスの定理で成り立っていた式を一般化したものです。ベクトルの大きさは一般にノルムと呼ばれます。
参考:ユークリッド空間R^Nの内積、ノルム、距離について解説
行列
数と数の間の単純な関係を考えるとき、中学校では1次方程式を考えました。
ベクトル同士の単純な関係は、連立1次方程式をによって表されます。さらに、それは行列と呼ばれる数を行と列に分けて並べたものによって単純に表せます。一般的に考えると難しいので、まずは\((2,2)\)の正方行列を題材とすると良いでしょう。
参考:1次方程式を行列で解くメリット・方法・条件について、幾何学的に見る
行列とベクトル、行列と行列の間には「左側の行ベクトル かける 右側の列ベクトル」といった独特な積が定義されます。行や列の呼び方、積の計算には慣れるしかないでしょう。
行列の計算方法を知ると、1次関数\(f(x)=ax\)と同様に、\(f(x)=Ax\)をベクトルの変換として見ることができます。図形の拡大縮小、反転・回転、せん断を具体例で考えてみると良いでしょう。
参考:行列の積の定義はなぜあの形? 変換の合成として見る、回転行列とは? 導出と例、性質を紹介
以上、最短で学ぶ小中高の数学、大学数学向けに最低限復習しておきたいことを紹介してきました。
紹介した題材に関する簡単な計算ができるようになっていれば、大学の微積分・線形代数、高校の理科にはおよそ対応できるかと思います。
小中高の数学で何が必要か、素早く復習したいときに理解不足な話題は何かを確認するときに、この記事が役立てば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
PHP研究所 (2015-03-12T00:00:00.000Z)
¥855
数研出版 (2019-01-24T00:00:01Z)
¥1,070 (中古品)
数研出版 (2019-11-01T00:00:01Z)
¥1,809 (中古品)
数研出版 (2018-11-01T00:00:01Z)
¥5,499 (コレクター商品)
こちらもおすすめ
微積分・初等解析のスキルツリー:必要な中学・高校レベルの数学
初等代数・幾何・論理のスキルツリー:線形代数に必要な中学・高校数学