どうも、木村(@kimu3_slime)です。
小学校の算数で、分数同士の割り算はひっくり返してかける
\[ \begin{aligned}\frac{3}{4}\div \frac{2}{5}= \frac{3}{4}\times \frac{5}{2}\end{aligned} \]
と習ったと思います。
種々の計算ルールを明らかなものとして認めてしまえば、次のような計算から、ひっくり返してかける結果になることは見て取れます。
\[ \begin{aligned} \frac{a}{b}\div \frac{c}{d} &= \frac{\frac{a}{b}}{\frac{c}{d} }\\&= \frac{\frac{a}{b} \times b \times d }{\frac{c}{d} \times b \times d } \\&=\frac{a\times d }{b\times c } \\ &=\frac{a}{b }\times \frac{d} {c}\end{aligned} \]
分母、分子に\(b\times d\)をかけて、二重になった分数を整理しました。これで納得できるなら以降は読まなくて良いです(笑)。
では、なぜこんな風に計算して良いのでしょうか? そもそも、分数を分数で割るとはどういうことなのでしょうか。
今回は、そもそも分数とは何かということに立ち返り、丁寧にわかりやすく解説します。
ひっくり返す結果になる理由としては、ある分数の逆数は、その分母と分子をひっくり返した数になることが重要です。
\[ \begin{aligned} \frac{2}{5}\times \frac{5}{2}=1 \end{aligned} \]
分数とは何か:分数の定義
分数の割り算に納得できないときは、そもそも、分数とは何かが納得できていないのではないでしょうか。
分数は、数と数の割り算を略記したものです。
\[ \begin{aligned}\frac{1}{2} = 1\div 2, \quad \frac{3}{5} = 3 \div 5\end{aligned} \]
視覚的なイメージとしては、ケーキを\(2\)等分したときの\(1\)つなどと説明されるかと思います。しかし、そのイメージは計算には役立てづらいです。数式としては、割り算の略記なのです。
\(3 \div 5\)は、小学校では、割り算ができない、割り切れないなどと教えられることもあったでしょう。それはキリの良い数(\(1,2,3,\dots\)などの整数)にならないだけです。ここでの割り算\(\div\)は、割り切れる、割り切れないを考えていません。\(3 \div 5\)という式は、キリが良くなくても、何らかの数を表していると考えます。
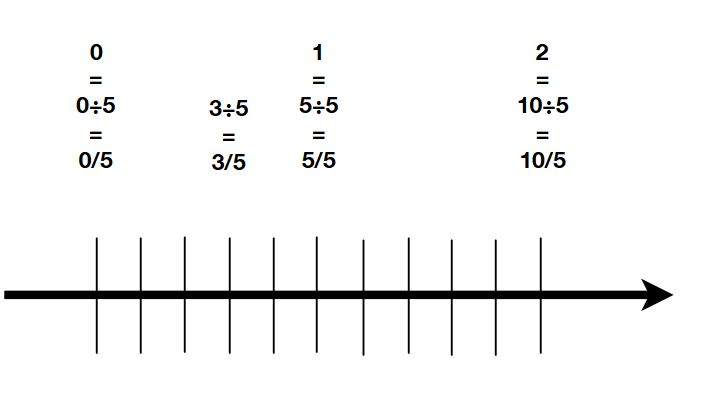
数を\(a,b\)と表すことにすれば、
\[ \begin{aligned}\frac{a}{b} := a\div b\end{aligned} \]
と「分数」\(\frac{a}{b}\)なる記号を、右辺(割り算)によって約束(定義)しています。\(a\)を分子、\(b\)を分母と呼びます。
どんな整数も、\(1\)を分母とした分数として表すことができますね。
\[ \begin{aligned} 2 = 2 \div 1 = \frac{2}{1},\quad a = a \div 1 = \frac{a}{1}\end{aligned} \]
割り算とは何か:掛け算の逆
分数とは、2つの数の割り算の略記であると。そうだとしたら、問題になるのは、割り算の計算方法です。割り算とは何なのでしょうか。これが分数の割り算を理解するための、重要なポイントです。
割り算とは、掛け算を逆にした計算のことです。どういうことでしょうか?
これは、引き算が足し算を逆にした計算であることに似ています。
例えば、\(2+ 3= 5\)という足し算は正しいです。そして、両辺から\(3\)を引けば、左辺は\(2+3-3= 2+0 =2\)なので、\( 2 = 5-3\)になります。
逆に言えば、\(5-3=2\)という引き算が正しいかどうかは、\(2+3=5\)が正しいかどうかによって約束されているわけです。これが、足し算と引き算が逆の計算であることの意味です。
より一般には、\(a-b=c\)とは、\(a= c+ b\)が正しいこと、と約束されます。
どのような数\(a\)に対しても、\(a-a=0\)です。なぜならば、\(a= 0+ a= a\)は正しいからですね。
では、\(6 \div 3=2\)が正しいのはなぜでしょうか? ここまで来れば、類推できるのではないでしょうか。
そう、\(6 = 2 \times 3\)が正しいからです。この式が正しいとき、両辺を\(3\)で割ってみましょう。左辺は\(6\div 3\)で、右辺は\(2 \times 3 \div 3= 2\times 1= 2\)です。
文字を記号で表せば、\(a\div b = c\)とは、\(a = c \times b\)が正しいことです。
こうすれば、どのような数\(a\)に対しても、\(a \div a=1\)です。なぜならば、\(a = 1 \times a\)が正しいからですね。
\(a \div a= 1 \div a \times a=1\)の両辺に\(b\)を掛ければ、
\[ \begin{aligned}b \div a \times a = b\times 1 = b \end{aligned} \]
\[ \begin{aligned} b \times \frac{a}{a} = b\times 1 = b \end{aligned} \]
つまり、同じ数を割って掛ける(掛けて割る)ことは、1をかける(値を変えない)ことと同じです。
重要なのは、割り算の式がわからなければ、掛け算の式に戻してみるということです。分数の割り算も、掛け算の式になおしてみれば理解できます。やってみましょう。
ひっくり返してかける理由
ここまでくれば、分数の割り算でひっくり返してかける理由がわかります。
まず、整数同士の割り算でも、分数の定義から、既にひっくり返すような形になっていることに注目してみてください。
\[ \begin{aligned} 1\div 2 = \frac{1}{2} , \quad 3 \div 5 = \frac{3}{5},\quad a \div b = \frac{a}{b}\end{aligned} \]
これがなぜ正しいかと言えば、分数\( \frac{1}{2}, \frac{3}{5}\)という記号を割り算で定義したからです。これが分数を扱うための、最初のルールです。
これは分数の掛け算のルールも与えてくれます。同じ数を掛けて割ると1になることを思い出せば、
\[ \begin{aligned} \frac{1}{2} \times 2= 1 \div 2 \times 2 = 1 \times 1 =1\end{aligned} \]
\[ \begin{aligned} \frac{3}{5} \times 5= 3 \div 5 \times 5 = 3 \times 1 =3\end{aligned} \]
\[ \begin{aligned} \frac{a}{b} \times b= a \div b \times b = a \times 1 =a\end{aligned} \]
です。さらに、両辺を分子で割れば、
\[ \begin{aligned} \frac{1}{2} \times 2 \div 1 = \frac{1}{2}\times \frac{2}{1}= 1 \div 1 =1\end{aligned} \]
\[ \begin{aligned} \frac{3}{5} \times 5 \div 3 = \frac{3}{5}\times \frac{5}{3}= 3 \div 3=1\end{aligned} \]
\[ \begin{aligned} \frac{a}{b} \times b \div a = \frac{a}{b} \times \frac{b}{a} =a \div a =1\end{aligned} \]
となります。掛けると\(1\)になる2つの数は、互いに逆数であると呼ばれるのでした。\(\frac{1}{2}\)は\(2\)の、\(\frac{3}{5}\)は\(\frac{5}{3}\)の、\(\frac{a}{b}\)は\(\frac{b}{a}\)の逆数です。
ある分数と、その分子分母を入れ替えた数は、互いに逆数です。
\[ \begin{aligned}\frac{a}{b} \times \frac{b}{a} =1\end{aligned} \]
また、両辺を\(\frac{b}{a}\)で割れば、
\[ \begin{aligned}\frac{a}{b} =1 \div (\frac{b}{a}) = \frac{1}{\frac{b}{a}}\end{aligned} \]
この式は、分数の掛け算、割り算の計算を簡単にしてくれます。
続いて、割られる数は整数のまま、割る数が分数になったときを考えてみましょう。
\[ \begin{aligned} 1 \div \frac{3}{5} =1 \times \frac{5}{3}\end{aligned} \]
です。ひっくり返して掛ける式になっています。
これはなぜなのでしょうか? これは逆数の式に立ち戻れば簡単です。まず、
\[\frac{3}{5} \times \frac{5}{3} =1\]
です。この式で両辺を\(\frac{3}{5}\)で割れば、左辺と右辺を入れ替えて
\[\begin{aligned} 1 \div \frac{3}{5} &= \frac{3}{5} \times \frac{5}{3} \div \frac{3}{5} \\ &= \frac{3}{5} \div \frac{3}{5} \times \frac{5}{3} \\ &= 1 \times \frac{5}{3}\end{aligned} \]
となります。
ここまでくれば、なぜひっくり返して掛けるかがわかりますね。分子、分母を文字で表すとして、
\[ \begin{aligned}\frac{a}{b}\div \frac{c}{d}= \frac{a}{b}\times \frac{d}{c}\end{aligned} \]
、ひっくり返して掛ける式を証明しましょう。
まず、\(\frac{c}{d}\)の逆数は\(\frac{d}{c}\)だったので、
\[ \begin{aligned} 1 =\frac{c}{d}\times \frac{d}{c}\end{aligned} \]
が成り立ちます。ここで両辺を\(\frac{c}{d}\)で割れば、
\[ \begin{aligned}1 \div \frac{c}{d} =1 \times \frac{d}{c} \end{aligned} \]
よって、両辺に\(\frac{a}{b}\)を掛ければ、
\[ \begin{aligned}\frac{a}{b} \div \frac{c}{d} =\frac{a}{b} \times \frac{d}{c} \end{aligned} \]
が得られました。
まとめ
少し長くなったので、まとめましょう。
分数とは、2つの整数の割り算のこと \[ \begin{aligned}\frac{a}{b} := a\div b\end{aligned} \]
割り算の逆は掛け算となることから
\[ \begin{aligned}\frac{a}{b} \times \frac{b}{a} =1\end{aligned} \]
つまり、分数\(\frac{a}{b}\)の逆数は\(\frac{b}{a}\)であることが示せる。
逆数の性質から、分数の割り算はひっくり返して掛けることが言える。
\[ \begin{aligned}\frac{a}{b}\div \frac{c}{d}= \frac{a}{b}\times \frac{d}{c}\end{aligned} \]
のでした。
ひっくり返す理由は、逆数の式\(\frac{a}{b} \times \frac{b}{a} =1\)に由来しています。これはより簡単なケースで言えば、
\[ \begin{aligned} a \times \frac{1}{a}= 1\end{aligned} \]
\[ \begin{aligned}1 \div a = \frac{1}{a}\end{aligned} \]
つまり、\(a \div a =1, 1 \times a =a\)に戻ります。これは常に正しいですよね。だから、そこから導ける分数の割り算の計算法則も正しいのです。
分数の割り算を学び初めの頃は、今回のような理屈は、飲み込みづらいかもしれません。
まずは簡単なケースから計算してみると良いでしょう。\[ \begin{aligned} 2 \times \frac{1}{2}= 1\end{aligned} \]など、逆数の式をたくさん計算してみれば、ひっくり返して掛ける式も、自然と納得できるようになると思います。
中学校以降の数学では、割り算\(\div \)の記号をあまり使わなくなります。それは、分数\[ \begin{aligned}\frac{a}{b} = a\div b\end{aligned} \]の記号によって割り算を表しているからです。「分数=分子を分母で割ったもの」という理解をすれば、数学でもつまづきにくくなるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
なぜ足し算より掛け算を先に計算するのか:交換法則、分配法則の視点