自然数の掛け算の交換法則が成り立つのはなぜか：定義と証明

どうも、木村（@kimu3_slime）です。

ネットでは小学校のかけ算の順序問題がしばしば話題になっているのを目にします。

今回はそれに立ち入らず、数の性質としての掛け算の交換法則に注目しましょう。掛け算九九を学ぶときには、

\[ \begin{aligned}5 \times 9 = 9 \times 5 =45\end{aligned} \]

のような交換法則に、自然と気づくことでしょう。

掛け算九九に限らず、そもそも掛け算の交換法則が成り立つのはなぜなのでしょうか？　それを簡単かつ丁寧に紹介したいと思います。

自然数、足し算、掛け算の定義
掛け算の交換法則の証明
こちらもおすすめ

自然数、足し算、掛け算の定義

今回考えるのは、\(0,1,2,3,\dots\)といった自然数です。文脈によって0を含めないことも多いですが、ここでは含めることにします。

理論的には、自然数はペアノの公理と呼ばれるルールによって定義されるものです。

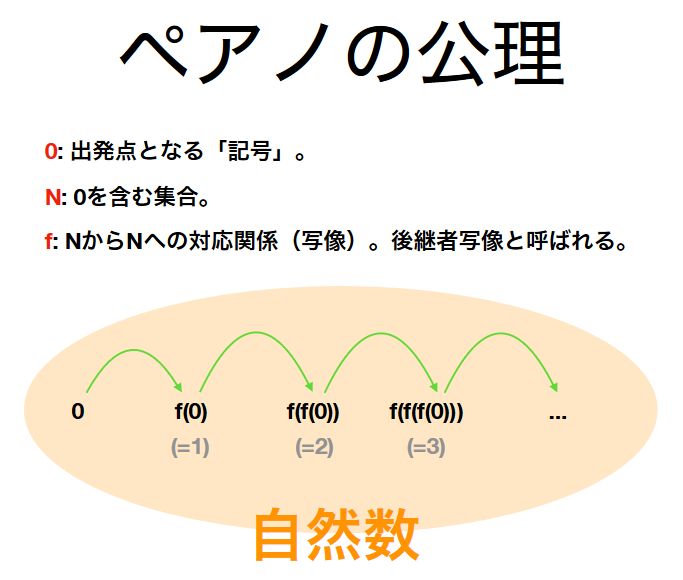
まず、出発点となる\(0\)という「数」がある。\(0\)に対してその「次」の数\(f(0)\)があるので、それを\(1:= f(0)\)と書く。1の「次」の数を2と書く。おおざっぱに言えばこんな感じのルールです。

詳しくは：数を「作って」みよう　近代数学と数概念の自由さについて – Share Studies

今回は、ペアノの公理そのものには踏み込みません。詳しくやると難しくなるので。自然数とは、ドミノ倒し的に、帰納的に定まった数の集まりなんだな、と思ってもらえば良いです。

自然数に対しては、足し算と掛け算を定義することができます。

足し算は、\(m,n,k\)を自然数として

0との和：\(m+0 =m\)
交換法則：\(m+n= n+m\)
結合法則：\((m+n)+k = m+(n+k)\)

を満たします。例えば、\(5+0 =5\)であり、\(2+5 =5+2=7\)であり、\((1+3)+5= 1+(3+5)=9\)です。今回は、こうした足し算の法則は成り立つものとして話を進めましょう。

掛け算は、次の条件を満たすように定義されます。（厳密に言えば、次の条件を満たす写像＝掛け算が、ただひとつ存在することが、ペアノの公理から示せます）

0との積：\(m\times 0 =0\)
掛け算と足し算の関係：\(m \times (n+1)= m+ (m\times n)\)

どんな自然数に0をかけても0になる。このルールは良いでしょう。

「掛け算と足し算の関係」のルール\(m \times (n+1)= m+ (m\times n)\)は、\(m\)を\(n+1\)回かけるということは、\(m\)を\(n\)回かけたもの\(m\times n \)に\(m\)を加えたものに等しい、という掛け算そのものの定義です。

もう少し具体的に言えば、\(3 \times 2\)とは、\(3\times 1\)に\(3\)を加えたものです。で、\(3\times 1\)とは何かというと、\(3\times 0 =0\)に\(3\)を加えたものです。したがって、\(3\times 1 =3 \)、\(3\times 2 = 3+3\times 1=6\)である、といった掛け算の結果が導かれます。

掛け算の交換法則を示すために、準備として分配法則

\[ \begin{aligned}m \times (n+k)= m\times n + m \times k\end{aligned} \]

\[ \begin{aligned}(m +n)\times k= m\times k + n \times k\end{aligned} \]

を示しておきましょう。前半を、\(k\)に関する帰納法で示します。

\(k=0\)のときは、0との積の性質を使って

\[ \begin{aligned} m \times (n+0) &= m \times n \\&= m\times n +0 \\&=m\times n +m\times 0 \end{aligned} \]

なので、成り立ちますね。

\(\ell\)を任意の自然数として、\(k= \ell\)のとき\(m\times (n+ \ell) = m\times n +m \times \ell\)が成り立つと仮定しましょう。\(k= \ell +1\)のときを考えると、掛け算の定義、足し算の性質に注意して

\[ \begin{aligned} m \times (n+\ell+1)&= m+(m\times (n+\ell))\\ &= m + m\times n +m \times \ell \\&= m\times n +(m+m \times \ell) \\&=m\times n +m\times (\ell+1) \end{aligned} \]

が成り立ちます。よって、分配法則が一般に成り立つと言えました。

\((m +n)\times k= m\times k + n \times k\)も、\(n\)に関する帰納法で全く同様に示せます。

掛け算の交換法則の証明

いよいよ、今までに定義、証明してきたことを使って、掛け算の交換法則

\[ \begin{aligned}m\times n = n\times m\end{aligned} \]

を証明してみましょう。

あくまで使えるのは今までに提示したルールであり、例えば\(0\times m =0\)とは（まだ）言えていないことに注意しましょう。交換法則のように、当たり前に見えることを確かめようとしているのです。

まず、一方が0、\(n=0\)のときを考えます。0との積の性質から、\(m\times 0 =0\)です。また、掛け算と足し算の関係から、\(0\times m =0+(0\times (m-1)) = 0\times (m-1)\)です。これを繰り返せば（＝帰納法により）、\(0\times m = 0\times 0 =0\)となり、\(m\times 0 = 0 \times m\)が言えました。\(m=0\)のときも同様です。

続いて、\(m,n\)が1以上のときを考えましょう。\(n\)に関する数学的帰納法で示します。まず、\(n=1\)のときは

\[ \begin{aligned} m\times 1 &= m+ (m \times 0)\\ &= m+0 \\&=m \end{aligned} \]

で、

\[ \begin{aligned} 1\times m &= 1+(1 \times(m-1))\\&=1+1+(1\times (m-2)) \\&= m\end{aligned} \]

です（1を\(m\)回足した数は\(m\)。厳密に言えば\(m\)に関する帰納法）。したがって、\(m\times 1 = 1\times m\)を満たします。

\(n=k\)、\(k\)が自然数のとき、\(m\times k = k \times m\)が成り立つとしましょう。\(n= k+1\)のときを考えると、分配法則を使って

\[ \begin{aligned} m \times (k+1) &= m\times k+m\times 1\\&=k\times m +m\times 1 \\&=k\times m +1\times m\\ &= (k+1)\times m\end{aligned} \]

が成り立ちます。よって、すべての自然数\(n,m\)に対して、\(m\times n = n\times m\)が成り立つと言えました。

以上、自然数の掛け算の交換法則が成り立つのはなぜか、自然数の足し算や掛け算の定義に戻って証明してきました。

自然数の定義（ペアノの公理）の話は、大学数学の抽象代数学などで扱うことがあるでしょう。今回の話は松坂「代数系入門」の付録「自然数」を参考にしています。ここでは省略しましたが、足し算の交換法則でさえ、定義から証明できるものです。

今回のような基礎的な話を知らなくても、掛け算の交換法則は当たり前に成り立ち、使って良いものです。ただしその背景に、今回のように論理的に積み上げられた理論があり、交換法則すら証明できることを知っておくと、より安心感を覚えられるのではないでしょうか。

木村すらいむ（@kimu3_slime）でした。ではでは。