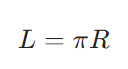どうも、木村(@kimu3_slime)です。
今回は、ユークリッド幾何学のロードマップ、論理関係のまとめをひとつの画像にしました。小中高校で学ぶ図形、幾何の分野をまとめた図としても、参考にどうぞ。
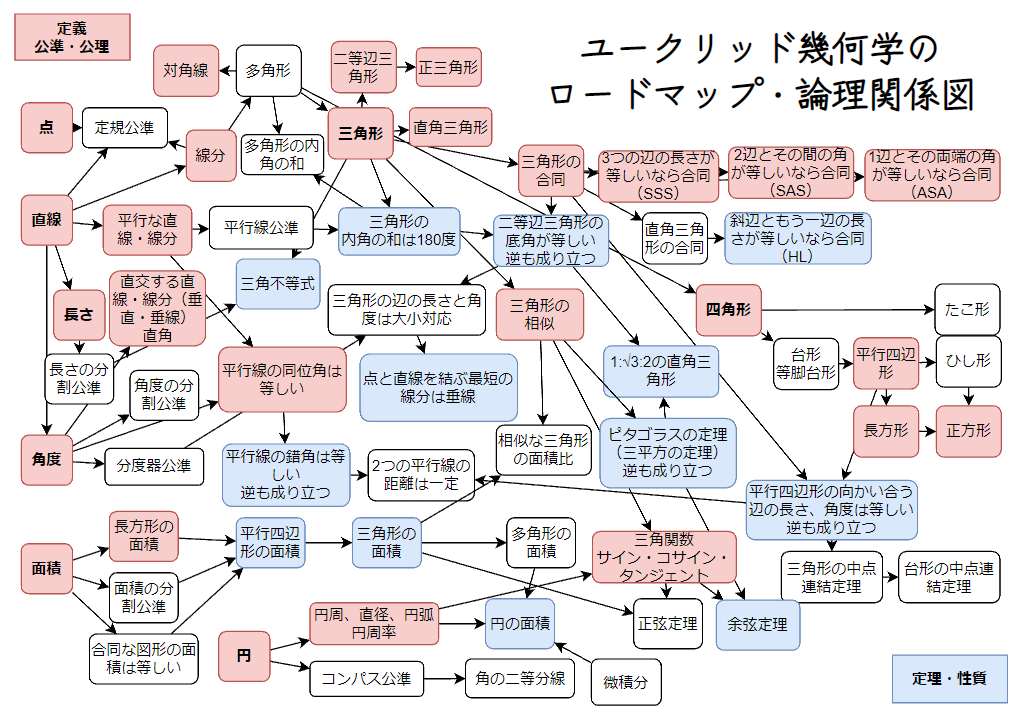
左上側に定義や公準・公理(議論の出発点)、右下側にそれらから導かれる定理や性質を配置しています。定義や公準は主に「Elementary Geometry for College Students」に基づいたものです。
色がついた項目を特に重要だと考えています。また、円、軌跡、立体図形関係は、中学高校で扱う内容であっても省略しています。
この図はかなり省略して描いています。矢印がないことが、論理関係が成立しないことを意味するわけではないことに注意。
以降、当サイトで紹介したユークリッド幾何学の記事を、分野ごとにまとめておきます。
点、直線
角度、平行、垂直
三角形、合同
三角形の内角の和が180度であることの証明:補助線、平行線公準を用いて
二等辺三角形の頂角の二等分線によってできる三角形は合同であることの証明
直角三角形の合同条件:斜辺ともう一辺の長さが等しいなら合同(HL)の証明
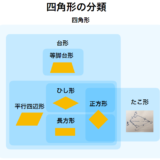
四角形
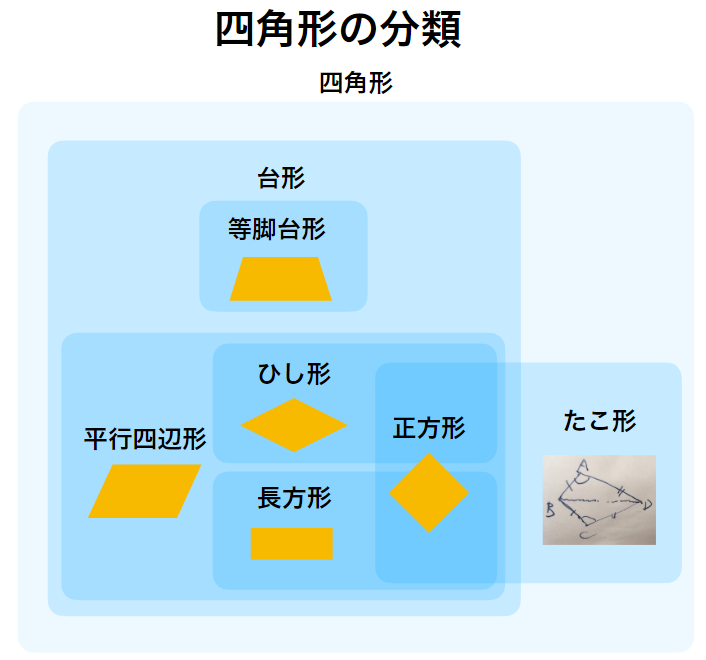
平行で長さの等しい2つの辺を持つ四角形は平行四辺形であることの証明
たこ形四角形の定義、大きさの等しい向かい合う角があることの証明
三角形の相似、ピタゴラスの定理、三角関数
面積
立体幾何、体積
公準「共線的でない3点に1つの平面が定まる」とは:基底による説明
公準「平面上の異なる2点を含む直線は平面内にあること」の線形代数による説明
その他・発展
多角形の対角線の本数の求め方:n(n-3)/2となることの証明
円周と直径の比が一定になるのはなぜか:円周率の三角関数による定義
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)
こちらもおすすめ
初等代数・幾何・論理のスキルツリー:線形代数に必要な中学・高校数学