どうも、木村(@kimu3_slime)です。
直角三角形の合同条件として、斜辺ともう一辺の長さが等しいなら合同(HL)があります。今回は、より一般的な三角形の合同条件からの証明を紹介します。
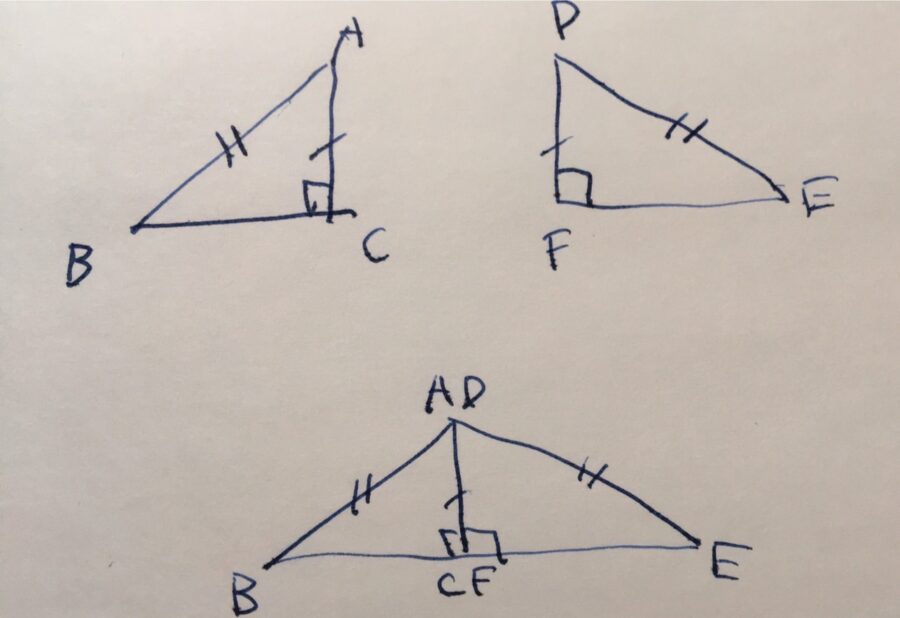
2つの直角三角形があり、その斜辺(hypotenuse)と他の一辺(底辺 leg)が等しいとしましょう。
例えば、\(\triangle ABC\)と\(\triangle DEF\)があり、\(\angle ACB = \angle DFE\)が直角、斜辺の長さが等しく\(AB= DE\)、もう一辺の長さも等しい\(AC = DF\)とします。
このとき、2つの三角形は合同です。この直角三角形の合同を示す方法には、HL(Hypotenuse Leg)という略称があります。
では、証明していきましょう。2つの辺の長さとその間の角度が等しいという条件に持ち込む方針です。
上の図のように三角形を平行移動・回転・反転させ(運動)、長さの等しい底辺を重ねてできるような大きな三角形\(\triangle ABE\)を考えます。
2つの三角形が直角三角形であるから、\(BE\)が折れ線でなく直線となり、三角形ができることに注意しましょう。
斜辺の長さが等しいという仮定\(AB= DE\)から、\(\triangle ABE\)は二等辺三角形です。
一般に、二等辺三角形の底角の大きさは等しいので、\(\angle ABC= \angle DEF\)となります。
また、三角形の内角の和は180度なので、
\[\angle ABC + \angle BCA + \angle CAB = 180^\circ\]
\[\angle DEF + \angle EFD + \angle FDE = 180^\circ\]
です。2組の角度が等しいことから、\(\angle CAB = \angle FDE\)が導けます。
よって、\(AB= DE\)、\(AC = DF\)、\(\angle CAB = \angle FDE\)となりました。三角形の合同条件、2つの辺の長さとその間の角度が等しい(SAS)から、\(\triangle ABC\)と\(\triangle DEF\)が合同であることが示せました。
以上、直角三角形の合同条件:斜辺ともう一辺の長さが等しいなら合同(HL)の証明を紹介してきました。
角度の情報を引き出すために、二等辺三角形に持ち込むのがポイントでしたね。
直角三角形の合同条件と呼ばれるものも、基本的な三角形の合同条件から導けることを知ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)
こちらもおすすめ
三角形の内角の和が180度であることの証明:補助線、平行線公準を用いて