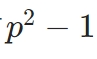どうも、木村(@kimu3_slime)です。
今回は、三角形の内角の和が180度であることの証明、それに平行線公準を用いていることを紹介します。
三角形は、(直線上にない)3点\(A,B,C\)によって決まる図形です。
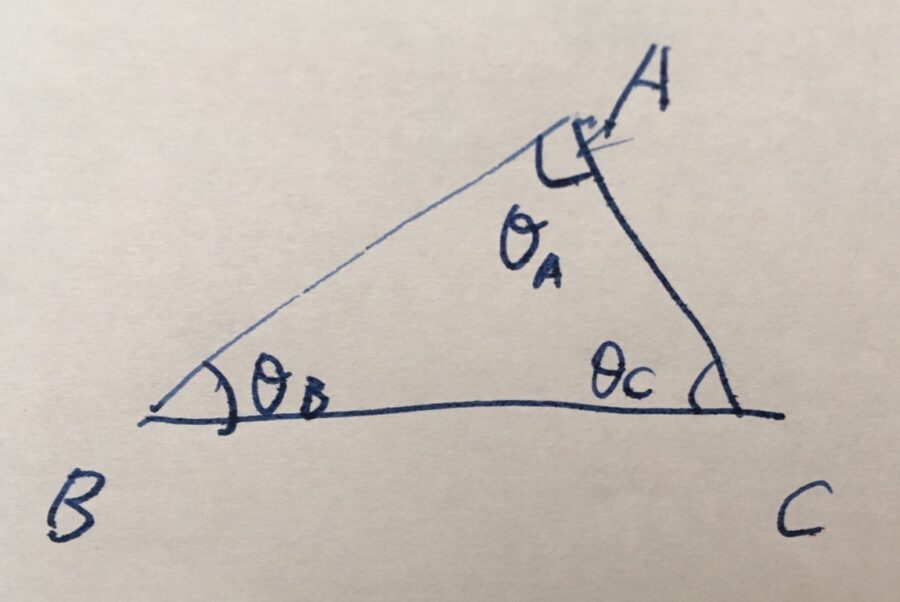
どんな三角形を考えても、内角\(\theta_A,\theta_B , \theta_C\)の和は
\[\theta_A +\theta_B + \theta_C=180^{\circ}\]
となります。
これを証明しましょう。
そのために、ある辺に平行な直線、今回は点\(A\)を通り線分\(BC\)に平行な直線を引きましょう。
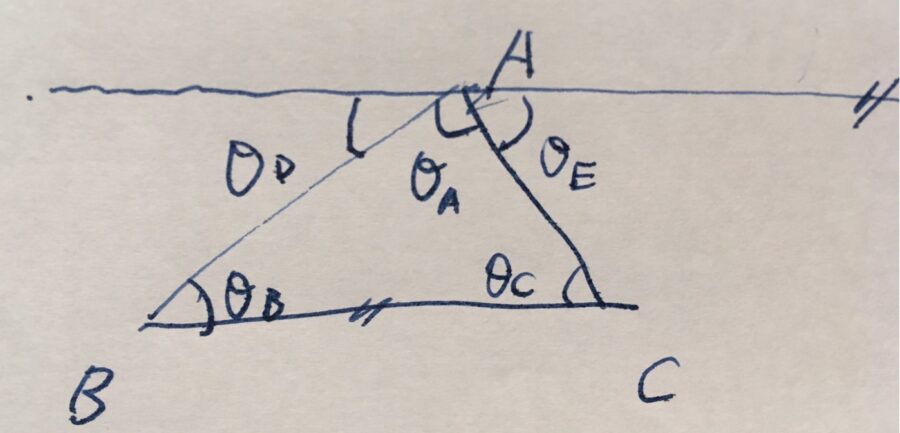
この「平行な線を引く」には、ユークリッド幾何学の議論の出発点:公準を用いています。「ある点を通り、ある直線(線分)に平行な直線がただひとつ存在する」という公理は、平行線の公準と呼ばれるものです。
その存在が論理的に正当化された、証明に用いる追加の直線は、補助線(auxiliary line)と呼ばれます。
この補助線によってできる角度を、\(\theta_D, \theta_E\)としましょう。\(\theta_A,\theta_D ,\theta_E \)は直線を分かつ角度なので、直線の角度の定義から
\[\theta_A+\theta_D +\theta_E=180^{\circ}\]
です。一方で、\((\theta_D,\theta_B)\)、\((\theta_E, \theta_C)\)は、平行線の錯角の関係です。(平行線の同位角が等しいという公準のもとで)、錯角の大きさは等しいので、
\[\theta_D = \theta_B\]
\[\theta_E = \theta_C\]
です。以上をまとめれば、
\[\theta_A +\theta_B + \theta_C=180^{\circ}\]
となることが示せました。
以上、三角形の内角の和が180度であることの証明、それに平行線公準を用いていることを紹介してきました。
「180度になる」という事実を知っている人は多いと思いますが、その証明に平行線や錯角を利用していると知るとより納得しやすいでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)
こちらもおすすめ
公準「共線的でない3点に1つの平面が定まる」とは:基底による説明