公準「共線的でない3点に1つの平面が定まる」とは：基底による説明

どうも、木村（@kimu3_slime）です。

ユークリッド幾何学の議論の出発点、公準のひとつに「共線的でない3点に1つの平面が定まる」というものがあります。

ユークリッド幾何学では平面は未定義語ですが、カメラの三脚のように、3点あれば定まるようなものを平面と呼んでいるわけです。

今回は、線形代数の用語、基底の考え方を用いてそれを紹介します。

座標を用いて、3つの点\(O= (0,0,0), A=(0,1,1), B=(1,1,0)\)について考えましょう。このとき、それらを通る平面は、次の図のようになっています。

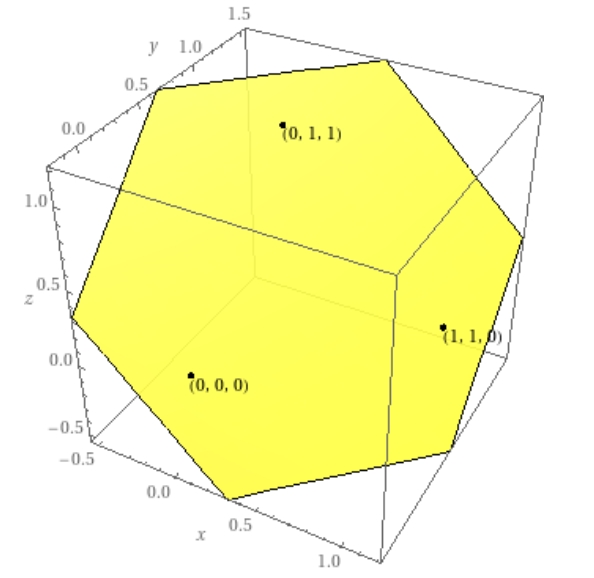
画像引用：WolframAlpha

3つの点を座標表示するときは、1つの点を原点\(O\)として考えれば、他の2点をそれを基準とした座標で表示することができますね。

3つの点が共線的でないとは、1つの点を原点として、他の点を表すベクトルが線形独立であることでした。

今回は、\(A,B\)は線形独立です。\(c_1A+c_2 B=0\)と仮定すると、第1成分の比較から\(c_2=0\)、第3成分の\(c_1=0\)が導かれるので。

したがって、これらのベクトルは平面（2次元の線形部分空間）を生成します。その基底は\(A,B\)で、\(O\)から\(A\)に直線的に向かう方向と、\(O\)から\(B\)に直線的に向かう方向を組み合わせて得られる点は、2次元的：平面上ですね。

より具体的には、この平面は\(z=-x+y\)と表せます。

一般的に「共線的でない3点に1つの平面が定まる」について考えましょう。

共線的でない3点とは、1つを原点とし、線形独立な2つのベクトルがあると考えられます。

そして線形独立な2つのベクトルは、2次元の線形部分空間：平面を生成します。

「1つの平面が定まる」についてですが、1つを原点とし、線形独立な2つのベクトルがあるとき、その3つが線形独立になることはありえません（原点＝ゼロベクトルは常に線形独立ではない）。\(A,B\)ベクトルの線形結合によってできる面以外の面は作れないわけですね（もしできたら、3点が線形独立となってしまう）。

「共線的でない3点」という条件ですが、もし1つだけが線形独立ならば、それらによって生成される線形空間は1次元：直線となります。直線をどうやって伸ばしても平面にはなりません。

以上、公準「共線的でない3点に1つの平面が定まる」とは何か、基底による説明をしてきました。

「2つの線形独立なベクトルによって1つの平面が作られる」と言い換えると、一般的に理解しやすくなるでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。