3つの点が共線的とは：線形独立性との関係

どうも、木村（@kimu3_slime）です。

今回は、3つの点が共線的とは何か、線形独立性との関係を紹介します。

ユークリッド幾何学において、3つの点が1つの直線上にあるとき、それらの点は共線的（colinear）であると呼ばれます。3つの点は共線を持つ、同一直線上にあるとも。

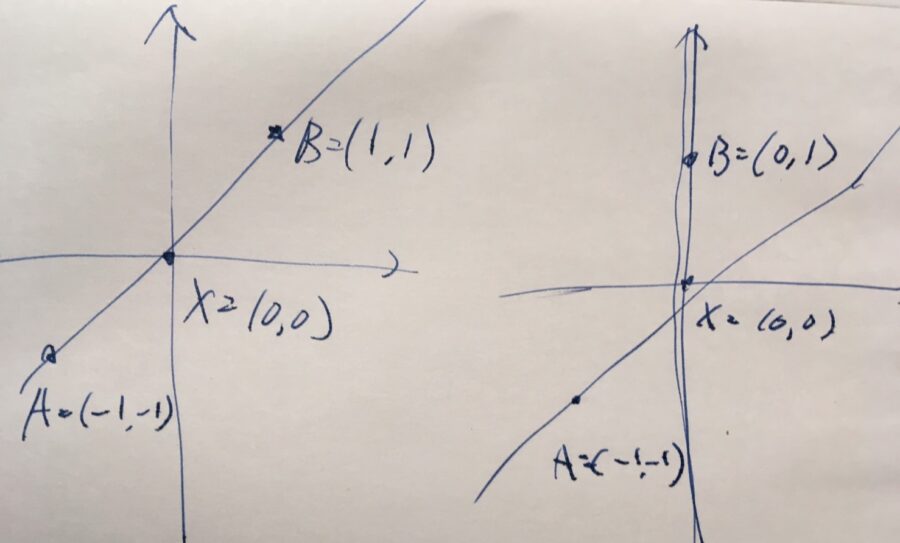
上の図の左側において、点\(A,X,B\)は共線的です。右側においては、共線的ではありません。

共線的な点からは三角形ができませんが、共線的でない点からは三角形が作れますね。線分の内分点や中点を考えるときには、それらが同一直線上にある：共線的でなくてはなりません。

この共線的という概念は、座標とベクトル、線形代数学における線形独立性によって言い換えることができます。

平面上の点は、座標（ベクトル）を使って表すことができます。

3つの点\(A,X,B\)が共線的であることは、それらのうち線形独立なものの個数が1つ以下（線形従属）であることです。

線形独立なベクトルの個数が1つのとき、例えば\(X = kA\)、\(B= \ell B\)といったように表せます。つまり、\(A\)というベクトルを定数倍したものが他の点\(X,B\)になっている、それは同じ直線上にあるということですね。

例えば、\(A=(-1,-1), X=(0,0),B=(1,1)\)のとき、これらは共線的です。実際、\(X= 0A\)、\(B= -1 A\)と表せるので、線形独立なベクトルは1個となります。

また、\(A=(-1,-1), X=(0,0),B=(0,1)\)のとき、これらは共線的ではありません。特に、\(A,B\)が線形独立ではありません。\(c_1 A+c_2 B=0\)を満たす数\(c_1,c_2\)があったとしましょう。両辺の成分を比較すると、\(-1c_1+0c_2 =0\)、\(-1c_1 +1c_2=0\)が成りたちます。したがって、\(c_1=c_2 =0\)が導かれるので、これらは線形独立です。

線形独立なベクトルの個数は、それらを並べた行列のランクと常に等しいという性質があります。\(A= (a_1,a_2),X=(x_1,x_2),B=(b_1,b_2)\)が共線的であるとは、行列

\[ \begin{pmatrix} a_1 &x_1&b_1\\ a_2 &x_2 &b_2 \end{pmatrix}\]

のランクが1以下である、とも言い換えられますね。

この考え方を用いれば、4つ以上の点が共線的とは何か、3次元や一般の次元における共線性も定義できます。

参考：線形独立・従属の判定法：行列のランクとの関係

以上、3つの点が共線的とは何か、線形独立性との関係を紹介してきました。

点が同じ直線上に並んでいるかという条件は幾何学において基本的ですが、座標やベクトルの言葉を使うとそれを一般的に表せることが伝われば嬉しいです。

木村すらいむ（@kimu3_slime）でした。ではでは。