多角形の対角線の本数の求め方：n(n-3)/2となることの証明

どうも、木村（@kimu3_slime）です。

今回は、多角形の対角線の本数の求め方、それが\(\frac{1}{2}n(n-3)\)となることの証明を紹介します。

多角形（polygon）とは、複数の点とその間をつなぐ線分（辺）からできた図形で、その線分は端点でしか交わらないようなもののことです。

多角形は頂点の個数に応じて呼び分けられ、三角形、四角形、五角形、一般に\(n\)角形があります。

多角形の対角線（diagonal）とは、隣接する（＝辺がある）頂点間でない、頂点間に引ける線分のことです。具体的に、対角線の個数\(D_n\)を数えてみましょう。

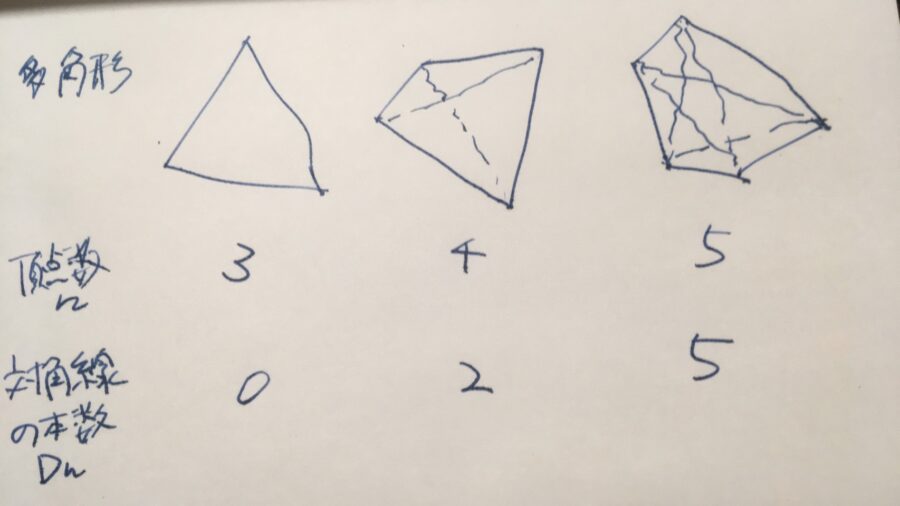
三角形は、すべての頂点が隣り合っているので、対角線はありません。四角形ならば2本、五角形ならば5本の対角線があります。

頂点数\(n\)が小さいうちは対角線を数えるのは簡単ですが、大きくなると図を書くのも難しくなります。実は、対角線の本数は、一般に簡単な形で

\[D_n = \frac{1}{2}n(n-3)\]

と表せます。ただし、\(n \)は\( n \geq 3\)を満たす整数です。

これは\(D_3 =0\)、\(D_4= 2\)、\(D_5 =5\)という結果にマッチしていますね。

また、例えば\(n=100\)ならば、\(D_{100}=50\times 97 =4850\)本と計算できます。

では、

\[D_n = \frac{1}{2}n(n-3)\]

となることを証明しましょう。

1つの頂点に注目し、そこから引ける対角線の本数を考えます。1つの頂点に隣接する頂点は2個あり、さらにそれ自身へは対角線は引けないので、残りの\(n-3\)個の頂点に向けて対角線が引けます。

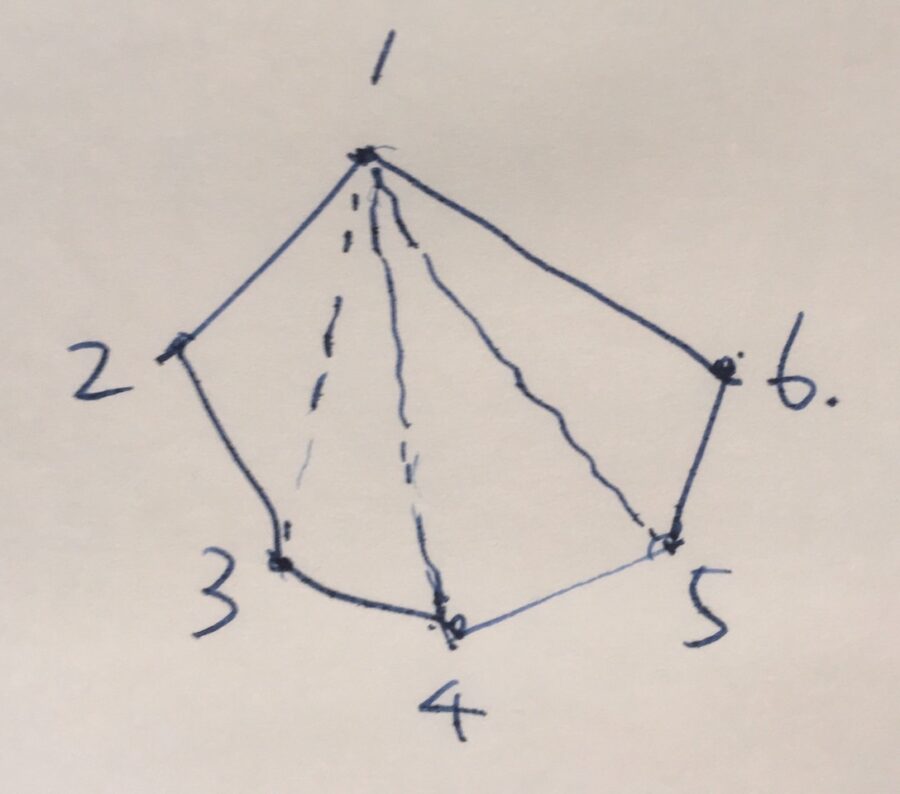
重複を気にせずに数えれば、\(n\)個の頂点から\(n-3\)本の頂点が引けるので、合計は\(n(n-3)\)本です。

ただし、対角線の\(\overline{13}\)（1から3への線分）と\(\overline{31}\)（3から1への線分）は同一であるように、2倍の重複があります。つまり、対角線の本数は\(n(n-3)\)の半分、\(\frac{1}{2}n(n-3)\)となることが示せました。

数学的帰納法によって証明することもできます。\(n \geq 3\)のとき、\(D_n = \frac{1}{2}n(n-3)\)を証明しましょう。

まず、\(n=3\)のときは、すべての頂点が隣接しているので、\(D_3 =0\)を満たします。

続いて、\(k\)を3以上の整数として、\(k\)角形の対角線の本数が\(D_k = \frac{1}{2}k(k-3)\)となると仮定します。

このとき、\(k+1\)角形を考えると、それは\(k\)角形に新たな頂点\(a\)を追加した図形として見ることができます。隣接する頂点\(b,c\)は2個なので、\(a\)からの対角線は新たに\(k-2\)本加わります。また、\(b,c\)間の1本の線分は、\(k\)角形としては辺ですが、\(k+1\)角形としては対角線なのでカウントしましょう。したがって、

\[\begin{aligned} D_{k+1} &= D_k + k-2 +1\\ &= \frac{1}{2}k(k-3)+\frac{1}{2}(2k-2) \\&= \frac{1}{2}(k^2 -k -2)\\&= \frac{1}{2}(k+1)(k-2)\end{aligned}\]

となり、確かに\(n=k+1\)のときも等式が成りたちます。

よって、数学的帰納法により、\(D_n = \frac{1}{2}n(n-3)\)が成り立つことが示せました。

組み合わせの考え方を用いると、より簡単です。

頂点間の線分は、\(n\)個の頂点から2個の頂点を選ぶ組み合わせによって決まるので、合計は

\[\begin{aligned} C(n,2) = \frac{1}{2}n(n-1) \end{aligned}\]

です。このうち\(n\)本は隣り合う頂点間の線分、つまり辺なので、それを除外したものが対角線の本数です。よって、

\[\begin{aligned} D_n &= C(n,2)-n\\&=\frac{1}{2}n(n-1)- \frac{1}{2}(2n) \\&= \frac{1}{2}n(n-3)\end{aligned}\]

となることが示せました。

以上、多角形の対角線の本数の求め方、それが\(\frac{1}{2}n(n-3)\)となることの証明を紹介してきました。

小さな多角形で数え方を考えれば、\(\frac{1}{2}n(n-3)\)という一般的な形は難しくなく導けるので、実験的に考えると良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。