同位角・錯角とは：平行線の錯角の大きさが等しいことの証明

どうも、木村（@kimu3_slime）です。

2つの平行線に交わる直線があるときに、

同位角は等しい
錯角は等しい

ことは平行線の性質として知られています。

今回は、同位角、錯角とは何か、「錯角が等しい」の「同位角が等しい」による証明を紹介します。

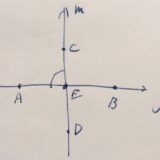
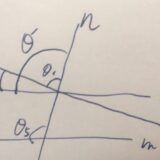
平行な直線\(\ell ,m\)とそれを横断する直線\(n\)があり、それらのなす角度を\(\theta_1,\dots , \theta_8\)としましょう。

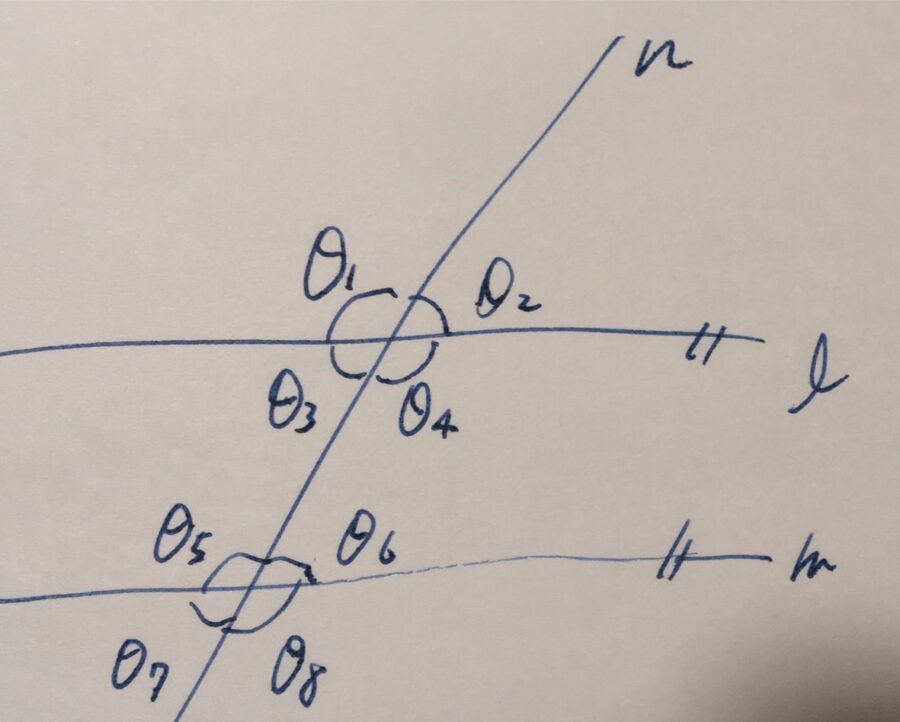
横断する直線に対して、相対的に同じ位置にある角を同位角（corresponding angle）と呼びます。

例えば、\((\theta_1, \theta_5)\)は互いに同位角です。\((\theta_2, \theta_6)\)、\((\theta_3,\theta_7)\)、\((\theta_4, \theta_8)\)もそうですね。2つの平行線があるとき、同位角の大きさが等しいことを、議論の出発点としましょう。

横断する直線に対して、相対的に反対側にある角を錯角（alternating angle）と呼びます。\((\theta_3,\theta_6)\)、\((\theta_4,\theta_5)\)は内側にある錯角です。外側にある錯角は、\((\theta_1,\theta_8)\)、\((\theta_2,\theta_7)\)ですね。

では、錯角が等しいこと、例えば内側の錯角について\(\theta_3 = \theta_6\)を証明しましょう。

一般に2つの直線が交わるとき、向かい合う角：対頂角は等しいです。したがって、\(\theta_3 = \theta_2\)となります。また、\(\theta_2 , \theta_6\)は同位角であり、同位角が等しいという前提から、\(\theta_2 = \theta_6\)です。これらを合わせて、\(\theta_ 3 = \theta_6\)がわかりました。

外側の錯角について、例えば\(\theta_1 =\theta_8\)を証明しましょう。

\(\theta_1 , \theta_5\)は同位角であり、同位角が等しいという前提から、\(\theta_1 = \theta_5\)です。\(\theta_5,\theta_8\)は対頂角なので、それらは等しくなります\(\theta_5 = \theta _8\)。よって、\(\theta_1 =\theta_8\)が示せました。

証明には「対頂角が等しいこと」を用いましたが、それは直線と角度の基本的な性質として証明できることです。

例えば\(\theta_1 = \theta _4\)を証明しましょう。\(\theta_1, \theta_3\)を合わせると直線になり、直線の角度は\(180^{\circ}\)としていることから、\(\theta_1+\theta_3 =180 ^{\circ}\)です。\(\theta_3, \theta_4\)も直線ができることから、\(\theta_3 +\theta_4 =180^{\circ}\)です。これらを合わせれば\(\theta_1 +\theta_3 = \theta_3+\theta_4\)で、\(\theta_3\)を両辺から引けば\(\theta_1 = \theta_4\)が導けました。

ユークリッド幾何学において、「同位角は等しい」ことは、証明できない議論の出発点：公準として知られています。

そこを出発点とすれば、錯角が等しいことが平行線の性質として証明できるわけですね。

今回と同じ議論をすれば、出発点を変えて「錯角が等しい」から「同位角が等しい」を導くこともできますね。しかしいずれにせよ、どちらか一方は事実として認めなければなりません。「錯角が等しいのはなぜ？同位角が等しいから」と「同位角が等しいのはなぜ？錯角が等しいから」の両方を用いるのは、循環論法です。

以上、同位角・錯角とは何か、平行線の錯角の大きさが等しいことの証明を紹介してきました。

僕は「同位角・錯角は等しいんだ」と中学校で習った記憶がありますが、一方を出発点とすればもう一方が導けるという流れを知ってもらえたら嬉しいです。

木村すらいむ（@kimu3_slime）でした。ではでは。