どうも、木村(@kimu3_slime)です。
2つの平行な直線について、
- 同位角は等しい(公準)
- 錯角が等しい
という性質があります。実はこの逆、2つの(平行かはわからない)直線があって
- 同位角が等しい
- 錯角が等しい
のいずれかを満たすならば、それらの直線は平行であると結論できます。今回は、その証明を紹介しましょう。
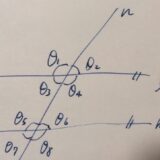
2本の直線\(\ell, m\)とそれを横断する直線\(n\)があるとし、そのなす角度を\(\theta_1,\dots, \theta_8\)とします。
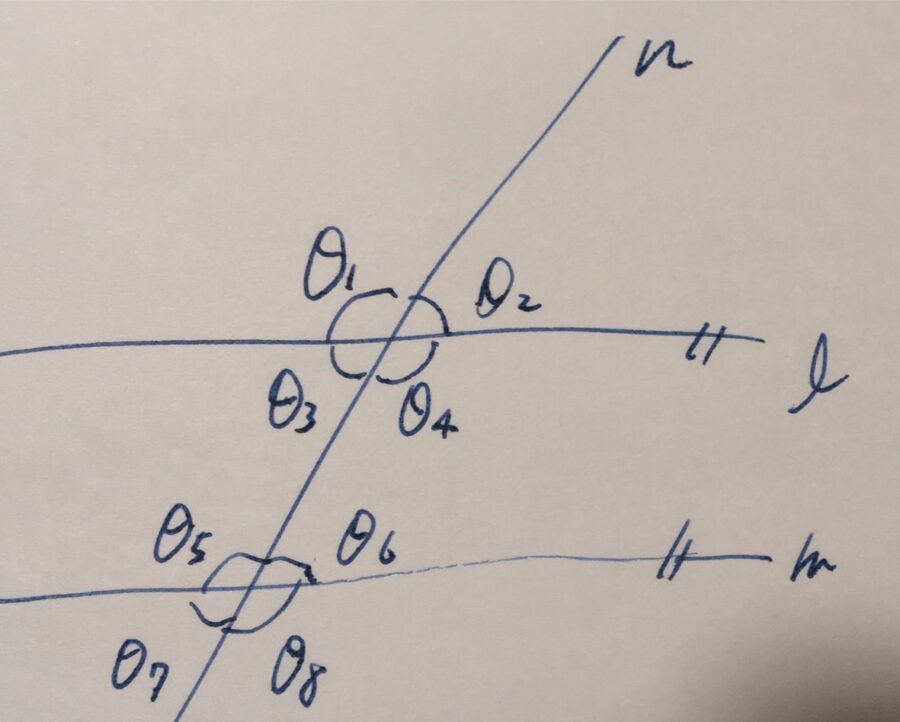
図では\(\ell ,m\)が平行であることを示す記号がついていますが、今回はそれを仮定しません。
同位角が等しいなら平行
それでも、同位角が等しい、例えば\(\theta_1 = \theta_5\)ならば、直線\(\ell ,m\)は平行であることを証明しましょう。仮定も結論の否定も正しいとすると矛盾が導かれること、背理法によって示します。
直線\(\ell ,m\)は平行でないと仮定しましょう。このとき、平行線の公準(1点を通りある直線と平行な直線が存在する)から、\(\ell ,n\)の交点を通り、\(m\)と平行な直線\(\ell ^{\prime}\)が存在します。
\(m\)の\(\theta_5\)に対応する\(\ell ^{\prime}\)の同位角を\(\theta^{\prime}\)としましょう。\(m,\ell^{\prime}\)は平行なので、平行線の同位角は等しい(公準)から、\(\theta_5 = \theta^{\prime}\)です。
一方で、仮定\(\theta_1 = \theta_5\)から、\(\theta_1 = \theta^{\prime}\)です。
さらに、\(\ell, \ell^{\prime}\)は平行ではありません(もし平行だとすると、\(\ell ,m\)が平行になり、仮定に反する)。したがって、「\(\theta_1+\theta^{\prime \prime} = \theta^{\prime}\)または\(\theta_1 = \theta^{\prime}+\theta^{\prime\prime}\)」となる角度\(\theta^{\prime\prime}\)が存在します。\(\ell ,\ell^{\prime}\)の上下によって角度の差の表現は変わりますが、いずれにせよ差があるわけです。
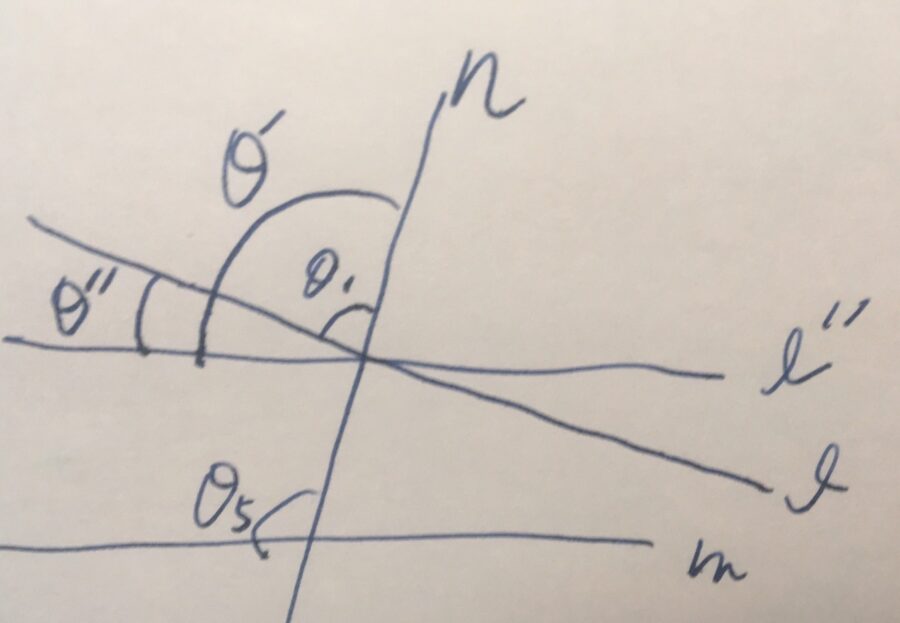
いずれのケースであっても、\(\theta_1 = \theta^{\prime}\)と合わせれば、\(\theta^{\prime \prime} =0\)です。これは同一でない直線のなす角度が正であること(分度器公準)、特に0でないことに矛盾します。
したがって「直線\(\ell ,m\)は平行でない」は偽であり、直線\(\ell ,m\)は平行でないことが示せました。
今回は\(\theta_1 = \theta_5\)のケースを考えましたが、他の同位角についても同様に示せます。
錯角が等しいなら平行
錯角が等しい、例えば\(\theta_3 =\theta_6\)ならば、直線\(\ell,m\)は平行であることを証明しましょう。
流れは先程とほぼ同様で、背理法によります。
直線\(\ell ,m\)は平行でないと仮定しましょう。このとき、平行線の公準(1点を通りある直線と平行な直線が存在する)から、\(\ell ,n\)の交点を通り、\(m\)と平行な直線\(\ell ^{\prime}\)が存在します。
\(m\)の\(\theta_6\)に対応する\(\ell ^{\prime}\)の錯角を\(\theta^{\prime}\)としましょう。\(m,\ell^{\prime}\)は平行なので、平行線の錯角は等しい(一般的性質)から、\(\theta_6 = \theta^{\prime}\)です。
一方で、仮定\(\theta_3 = \theta_6\)から、\(\theta_3 = \theta^{\prime}\)です。
さらに、\(\ell, \ell^{\prime}\)は平行ではありません。したがって、「\(\theta_3+\theta^{\prime \prime} = \theta^{\prime}\)または\(\theta_3 = \theta^{\prime}+\theta^{\prime\prime}\)」となる角度\(\theta^{\prime\prime}\)が存在します。
いずれのケースであっても、\(\theta_3 = \theta^{\prime}\)と合わせれば、\(\theta^{\prime \prime} =0\)です。これは同一でない直線のなす角度が正であること(分度器公準)、特に0でないことに矛盾します。
したがって「直線\(\ell ,m\)は平行でない」は偽であり、直線\(\ell ,m\)は平行でないことが示せました。
今回は\(\theta_3 = \theta_6\)のケースを考えましたが、他の錯角についても同様に示せます。
以上、平行線の性質の逆「同位角・錯角が等しい直線は平行」の証明を紹介してきました。
「平行線の同位角は等しい」を議論の出発点:公準として認めれば、「同位角(錯角)が等しい2つの直線は平行である」と逆の性質も必然的に成り立つわけですね。
まとめれば、2つの直線が平行であることは、2つの直線の同位角(錯角)が等しいことの必要十分条件(互いに同値)です。数学においては、これを「同位角(錯角)が等しいことは平行な直線を特徴づける」と言ったりします。
平行線と同位角・錯角の関係は、少ない原理から多くの性質が導ける例として、面白いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)