どうも、木村(@kimu3_slime)です。
今回は、球の体積でなぜ4/3が出るか:多面体による導出を紹介します。
半径\(r\)の球の体積\(V\)は、
\[V =\frac{4}{3}\pi r^3\]
によって求められます。
この式が成り立つ理由を説明するのは、積分を使うのが確実です。
今回は、それほど厳密ではありませんが、多面体による導出を紹介しましょう。
平面における円は、頂点数を増やした正多角形によって近似することができます。これによって、正多角形の面積の公式から、円の面積の公式が導出できます。
これと同じ発想で、球を面を増やした正多角形として近似してみましょう。(実際には、正多面体の面は20面以上はありえませんが、近似的なお話です。)
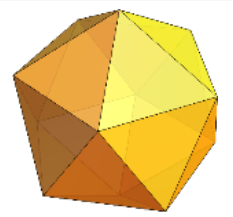
画像引用:WolframAlpha
球の面積が、\(n\)個の面を持つ正多面体によって近似できるとしましょう。

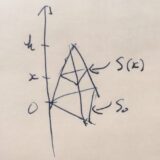
この正多面体の体積は、上の図のように、角錐の合計として捉えることができます。角錐の体積\(V_k\)は、底面積を\(S_k\)、高さを\(h\)とするとき、\(V_k = \frac{1}{3}S_k h\)でした。したがって、多面体の体積はそれらの合計であり、
\[V\simeq V_1+\cdots+V_n \\ = \frac{1}{3}(S_1+\cdots+S_k)h\]
となります。ここで面の数\(n\)を増やすと、底面積の合計\((S_1+\cdots+S_k)\)は球の表面積\(4\pi r^2\)、高さは球の半径\(r\)に近づくとしましょう。これらを当てはめれば、
\[V = \frac{1}{3}(4\pi r^2) r \\ =\frac{4}{3}\pi r^3\]
を導くことができました。
以上、球の体積でなぜ4/3が出るか:多面体による導出を紹介してきました。
厳密な話ではありませんが、球の表面積から\(4\pi r^2\)、角錐の体積から\(\frac{1}{3}S_k r\)が出る結果、\(\frac{4}{3}\)が導かれるという説明によって、体積の公式が納得しやすくなれば嬉しいです。
ただし、今回の議論で前提とした、表面積が\(4\pi r^2\)である理由も知りたければ、やはり微積分を学ぶ必要があるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)