正多角形の面積の求め方、証明

どうも、木村（@kimu3_slime）です。

今回は、正多角形の面積の求め方、その証明を紹介します。

正多角形の面積\(A\)は、

\[\begin{aligned} A &= \frac{1}{2}ap\\ &=\frac{1}{2} ans \end{aligned}\]

によって求められます。

ここで\(a\)は辺心距離、\(p\)は周長、\(n\)は頂点数、\(s\)は1辺の長さです。

辺心距離（apothem）とは、正多角形の中心と各辺との距離、つまり中心から辺への垂線の長さのことです。正多角形には、各頂点からの距離が等しい点＝中心がただひとつ存在します。各頂点から中心の距離が半径で、辺心距離は辺からの距離であることに注意しましょう。

周長は長さ\(s\)の辺が\(n\)個の合計なので、\(p=ns\)という関係があります。

例として正方形（正四角形）のケースで、この面積の求め方が正しいことを検証してみましょう。

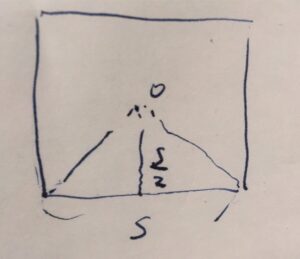
1辺の長さを\(s\)とすると、辺心距離は\(a= \frac{1}{2}s\)です。そして周長は\(p=4s\)となります。これらをさきほどの式に代入すると、

\[\begin{aligned} A &= \frac{1}{2}ap\\ &=\frac{1}{2} \cdot \frac{1}{2}s \cdot4s\\&=s^2 \end{aligned}\]

となり、確かに1辺の長さを使った正方形の面積の公式が導かれました。

では、一般的な正多角形の面積の求め方が正しいことを証明していきましょう。

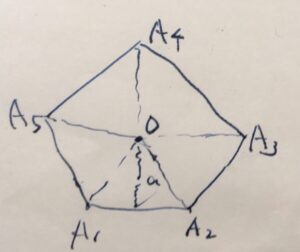
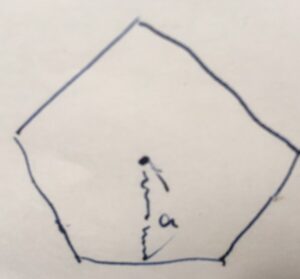
上の図では正五角形ですが、正\(n\)角形を考えます。

中心\(O\)から各頂点\(A_1,\dots,A_n\)に直線を引くと、\(n\)個の三角形ができあがります。

これらの三角形が、合同であることを示しましょう。

まず\(OA_1,OA_2\)などは中心から頂点への距離で、中心の定義からそれらは等しいです。また、中心角は\(\angle A_1 OA_2 = \frac{360^{\circ}}{n}\)と知られています。

よって、三角形の合同条件、2つの辺の長さとその間の角度が等しいから（SAS）、これらの三角形は合同です。

三角形ひとつの面積は、底辺かける高さ割る2なので、\(\frac{1}{2}as\)です。長さ\(s\)の辺を底辺とすると、辺心距離が垂線の長さ、すなわち高さに対応するので。合同な三角形の面積は等しいので、どの三角形の面積も\(\frac{1}{2}as\)となります。

正多角形の面積は、これら\(n\)個の三角形の面積の合計なので、

\[\begin{aligned} A &= \frac{1}{2}ans\\ &=\frac{1}{2} ap \end{aligned}\]

を示すことができました。

ちなみに、\(n\)を大きくしていくと、正多角形は円に近づいていきます。

辺心距離\(a\)が半径\(r\)に、周長\(p\)が円周\(2\pi r\)に近づいていくとして、この面積の求め方に当てはめると

\[A= \frac{1}{2} \cdot r \cdot 2\pi r =\pi r^2\]

となって、円の面積の公式が導けます。

厳密な話ではありませんが、円の面積の公式がなぜこの形なのかは、正多角形の面積の公式を知ると納得しやすいかもしれません。

以上、正多角形の面積の求め方、その証明を紹介してきました。

四角形や多角形の面積を調べるために、基本的なパーツとして三角形に分割するのが有効だと感じられますね。

木村すらいむ（@kimu3_slime）でした。ではでは。

posted with AmaQuick at 2022.05.16

()

￥13,970 (中古品)

こちらもおすすめ