30、60、90度の直角三角形の辺の長さの比の覚え方、証明

どうも、木村（@kimu3_slime）です。

今回は、30、60、90度の直角三角形の辺の長さの比の覚え方、証明を紹介します。

三角定規で馴染みのある直角三角形の辺の長さの比として、次の2つが有名です。

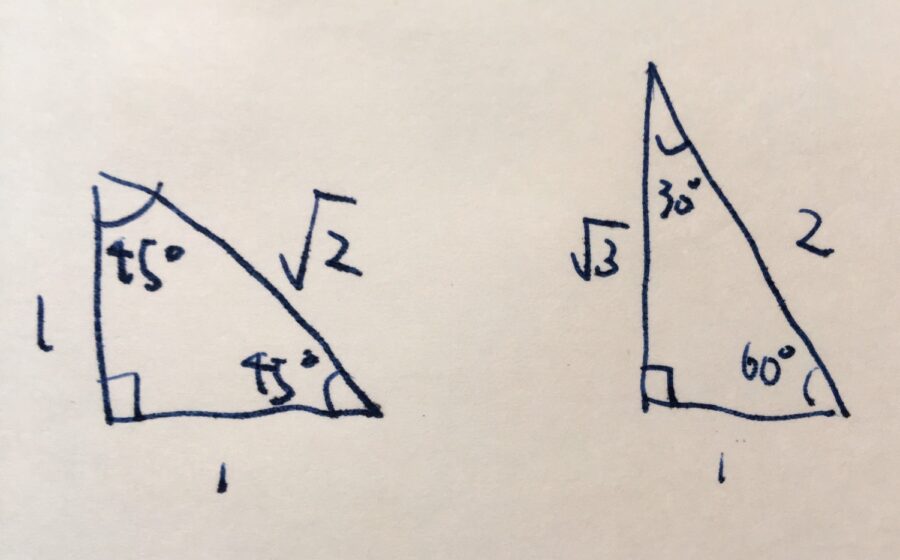
ひとつは、45、45、90度の直角三角形。辺の長さの比は、\(1:1:\sqrt{2}\)となります。2つの角度が等しいので、二等辺三角形となることがわかり、斜辺以外の辺の長さが等しいことがわかりますね。斜辺の長さは、ピタゴラスの定理により\(\sqrt{2}\)です。

もうひとつは、30、60、90度の三角形。辺の長さの比は、\(1:\sqrt{3}:2\)となります（一番最後が斜辺。\(1:2:\sqrt{3}\)という覚え方も有名だが、順序に注意）。

後者は一見すると、前者の二等辺三角形のようなわかりやすさがありません。辺の長さの比を結果として覚えるだけでなく、正三角形を半分にした形と知れば納得しやすいでしょう。

30、60、90度の三角形を見たら、次のように折り返した三角形をくっつけましょう。

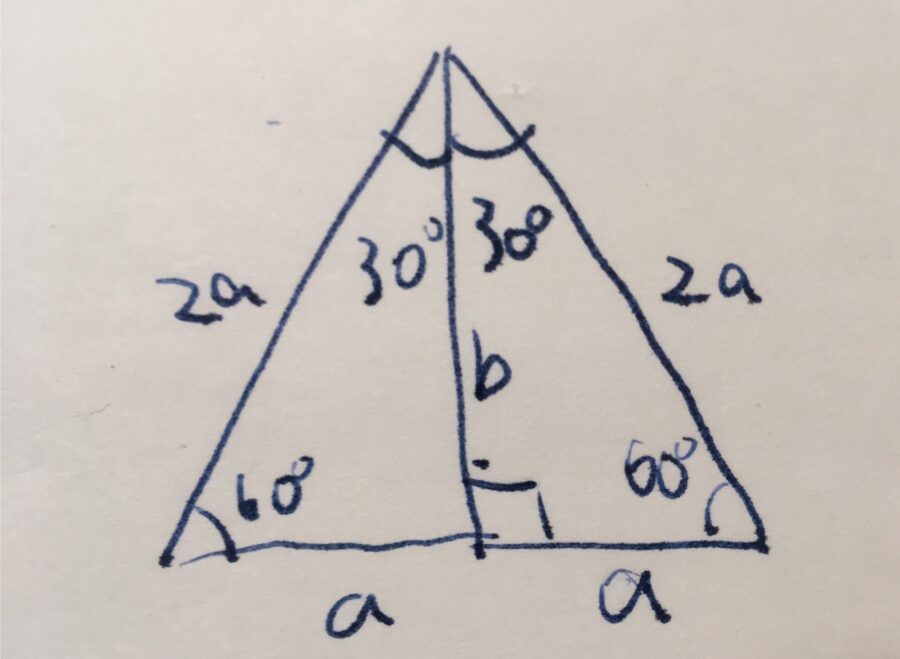
すると、全体としては、すべての角度が\(60^{\circ}\)の三角形、正三角形となります。

大原則として三角形の内角は\(180^{\circ}\)です。そして角度と長さの対応関係から、3つの角度が等しい：\(\frac{180}{3}=60\)度の三角形は、3つの辺の長さが等しい＝正三角形となるわけです。

辺の長さの比は、正三角形であることから導けます。

\(30^{\circ}\)の角に向かい合う、最も短い辺の長さを\(a\)としましょう。すると、反転した三角形の辺の長さも\(a\)なので、大きな正三角形の辺の長さは\(2a\)となります。

直角三角形部分に注目して、残りの辺の長さを\(b\)とします。ピタゴラスの定理から、\(a^2+b^2 =(2a)^2\)です。よって、\(b^2 = 3a^2\)、辺の長さは正なので、\(b= \sqrt{3} a\)となることがわかりました。

この辺の長さを比としてまとめると、\(a: \sqrt{3}a : 2 a =1:\sqrt{3}:2\)となります。

以上、30、60、90度の直角三角形の辺の長さの比の覚え方、証明を紹介してきました。

典型的な直角三角形の比の長さは、三角関数の典型的な値をスムーズに求めるためにも知っておく必要があります。

まずはピタゴラスの定理が大事で、30、60、90度の三角形は正三角形を作るとわかりやすくなりますね。

木村すらいむ（@kimu3_slime）でした。ではでは。

posted with AmaQuick at 2022.05.16

()

￥13,970 (中古品)

こちらもおすすめ