球面の幾何学入門：平行な直線が存在しないこと

どうも、木村（@kimu3_slime）です。

今回は、球面の幾何学入門ということで、平行な直線が存在しないことについて紹介します。

球面における直線とは
平行線が存在しないこと
こちらもおすすめ

球面における直線とは

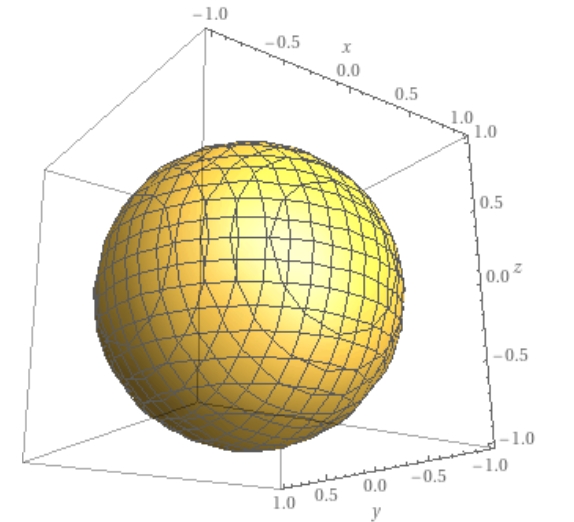
画像引用：WolframAlpha

3次元空間\(\mathbb{R}^3\)において、半径1の球面は\(x^2+y^2 +z^2 =1\)という方程式を満たす点の集まりです。これを

\[S^2 :=\{(x,y,z)\in \mathbb{R}^3 \mid x^2+y^2+z^2 =1\}\]

と書き、単位球面（unit sphere）と呼びます。

球面上の図形、幾何学について考えましょう。

平らな平面の幾何学（ユークリッド幾何学）では、直線から話が始まります。2つの点があるとき、それらを通る直線がある。球面上の直線とはなんでしょうか？

球面上の「直線」を、大円（great circle）として定義します。大円とは、単位球面と原点を通る平面の共通部分のことです。

平らな平面の幾何学では、ある平面と別の平面の共通部分が「直線」となっていました。この考え方を活かしたのが、大円を球面における直線とした定義です。大円は曲がっていますが、それでも球面における直線と呼びます。

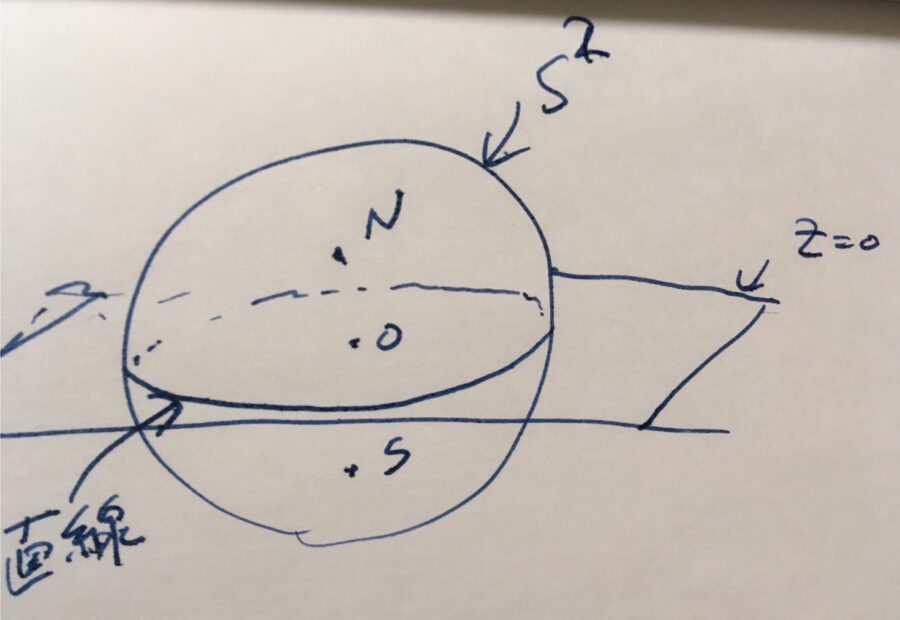
例えば、

\[\{(x,y,z) \in S^2 \mid z=0\}\]

は単位球面における直線です。\(N=(0,0,1)\)を北極、\(S=(0,0,-1)\)を南極と呼べば、この直線は赤道に対応するものですね。

（実は、大円は球面上の最短距離を実現する曲線：測地線になることが知られています。その意味でも、直線であるわけです。）

一般に、

\[\{(x,y,z) \in S^2 \mid ax+by+cz=0\}\]

が大円です。このように定義すれば、球面上の異なる2点に対し、少なくとも1つは直線（大円）が存在すると言えます。3つの未知数\(a,b,c\)に対し、2つの線形方程式が定まるので、これは常に解を持つわけです。

一般に、舞台となる集合と（一定の条件を満たした）「直線」の組を、抽象幾何（abstract geometry）と呼びます。

今回考えた単位球面と大円による直線の組\((S^2, \mathcal{L})\)は、抽象幾何の定義を満たします。特に、これは球面の幾何学（spherical geometry）、リーマン球（Riemann sphaere）と呼ばれます（リーマン幾何は他の意味を持つ用語であることに注意）。

ユークリッド幾何学では、異なる2点を通る直線はただひとつでした。こうした条件を満たす幾何学は、結合幾何（incidence geometry）と呼ばれます。

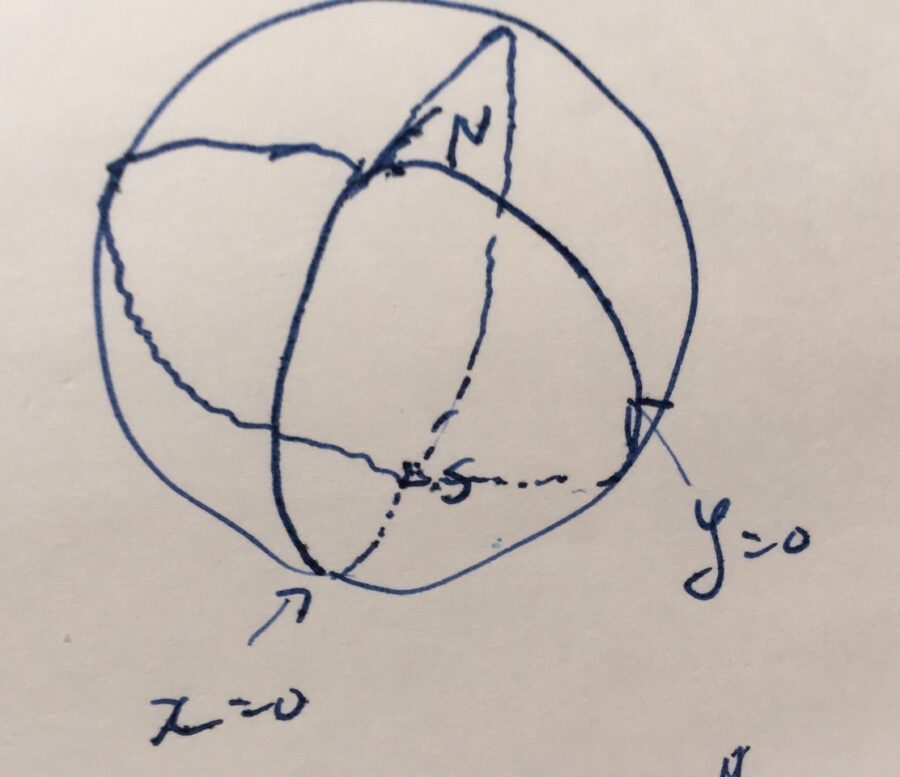
球面の幾何学では、異なる2点を通る直線は無数に存在します。例えば、北極と南極を通る直線として、

\[\{(x,y,z) \in S^2 \mid x=0\}\]

\[\{(x,y,z) \in S^2 \mid y=0\}\]

という2つを考えられます。\(N=(0,0,1)\)、\(S=(0,0,-1)\)はどちらもこれらの直線上にある点ですね。よって、球面上の幾何学は結合幾何ではありません。

平行線が存在しないこと

ユークリッド幾何学との違いとしては、平行線の公準の話が有名です。

ユークリッド幾何学においては、直線とその直線上にない点があるとき、その点を通りその直線に平行な直線が存在します。これは議論の出発点、平行線の公準と呼ばれるものです。これはユークリッド幾何学において、他の公理から証明できないものとして知られています。

球面の幾何学においては、直線上にない点を通る平行な直線は存在しません。2つの直線が平行とは、それらが交わらない（共通部分を持たない）ことです。

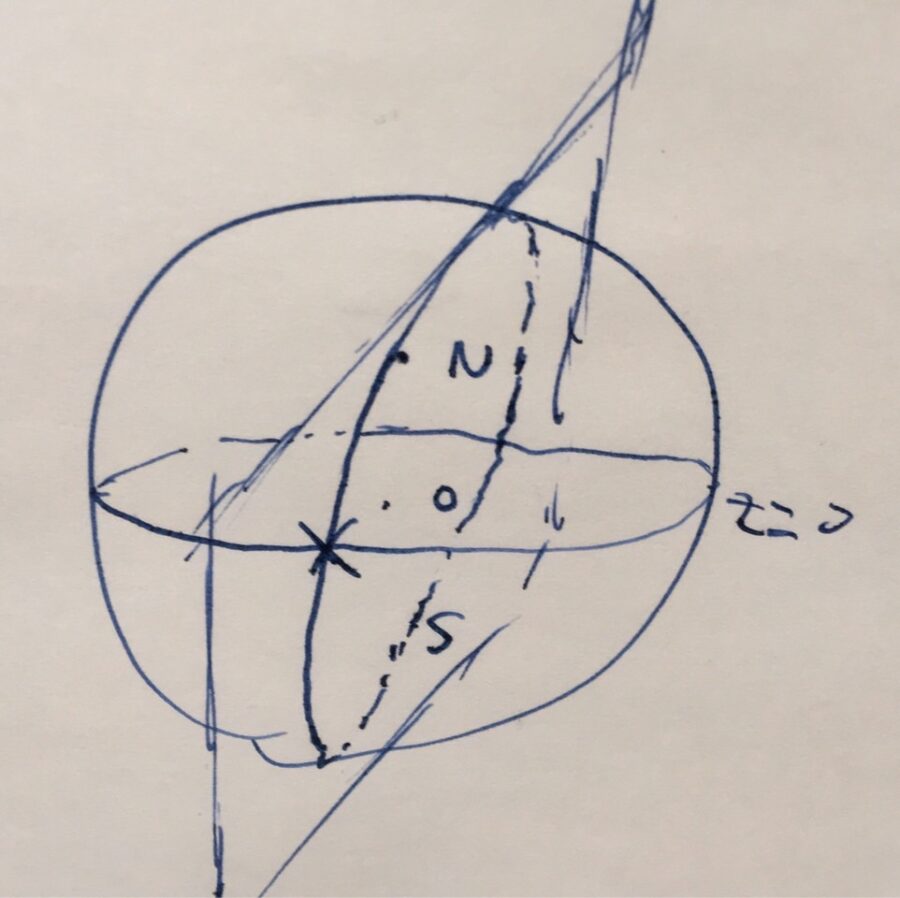
例えば、

\[\{(x,y,z) \in S^2 \mid z=0\}\]

という直線を考えましょう。そして、例えば直線上にない点\(N=(0,0,1)\)を考えます。\(N\)を通る直線、つまり大円は、\(N\)を通り原点を通る平面と球面の共通部分です。したがって、原点について対称な点、対蹠点（antipodal point）を通ります。北極の対蹠点は南極\(S=(0,0,-1)\)です。

\(N,S\)をつなぐ大円を考えると、球面は連結なので、その中間である\(z=0\)を通らざるを得ません。よって、直線上にない点を通る直線を考えると、それらは必ず交わる：平行でなくなることが示せました。

以上、球面の幾何学入門として、平行な直線が存在しないことについて紹介してきました。

球面における直線とは大円のこと、平行な直線とは交わらないことであると知れば、「球面の幾何学では平行な直線が存在しない」という文の意味がわかるようになりますね。

木村すらいむ（@kimu3_slime）でした。ではでは。