どうも、木村(@kimu3_slime)です。
今回は、直線と点を結ぶ最短の線分は垂線であることの証明を紹介します。
直線\(\ell\)と直線上にない点\(P\)を考えましょう。
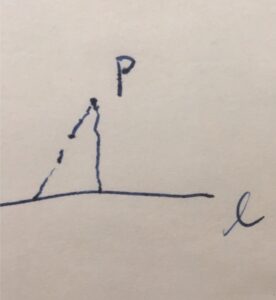
\(P\)と\(\ell\)上の点を結ぶ点は無数に考えられます。その中で最も短くなりそうなのはどんな線分でしょうか。それが垂線です。
\(\ell\)の垂線で、\(P\)を端点とする線分を考え、\(\ell\)側の端点を\(H\)としましょう。また、\(H\)以外の\(\ell\)上のいずれかの点を\(A\)とします。
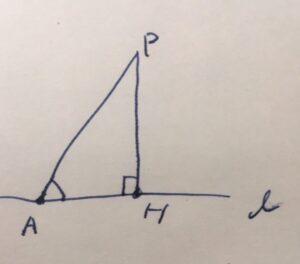
このとき、\(PH < PA\)となることが証明できます。方針としては、三角形の辺の長さと角の大きさの関係に持ち込みます。
三角形の内角の和は180度なので、
\[\angle AHP + \angle HPA + \angle PAH =180^\circ\]
です。\(PH\)は垂線なので\(\angle AHP =90^\circ\)であり、
\[\angle HPA + \angle PAH =90^\circ\]
となります。また、\(P,A,H\)は同一の直線上にないので、\(\angle HPA >0\)です(protractor postulate)。
よって、\(\angle PAH < 90^{\circ} \)です。不等式の性質(推移律)から、\(\angle PAH < \angle AHP\)となります。
したがって、三角形の辺の長さと角の大きさの対応関係から、\(PH <PA\)となることが示せました。
以上、直線と点を結ぶ最短の線分は垂線であることを紹介してきました。
この事実は、三角形の辺の長さに関する三角不等式の証明に用いる基本的な事実です。
垂直が最短というのは直観的には明らかですが、それが角度を通じて議論できるのは面白いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)