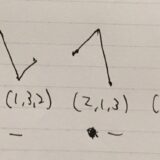
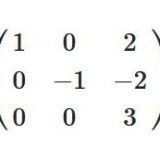
上三角、下三角行列の性質:積、逆行列、固有値について
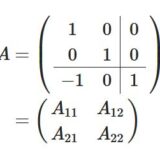
ブロック行列とは:ブロック対角行列の例と性質
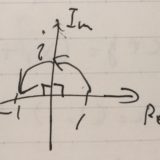
複素数と行列の対応関係:行列表現
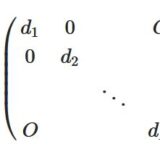
対角行列の性質:積、逆行列、固有値について
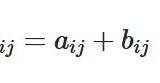
行列全体のなす集合が線形空間(ベクトル空間)となることの証明
なぜ平行でないベクトルによる分解を考えるか:線形独立とは
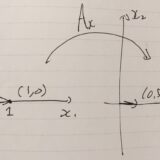
一次変換(線形変換)とは:点、直線の像の求め方

連続関数とは:イプシロンデルタと開集合、閉集合による特徴づけ
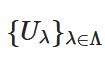
コンパクト性とは:有界閉集合、最大値の定理を例に
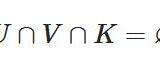
連結性とは:実数区間、中間値の定理を例に
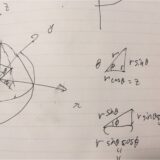
曲面のパラメータ表示、曲面積、球座標(3次元極座標)とは?
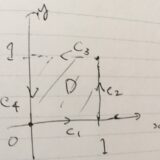
グリーンの定理の例による理解と証明、応用
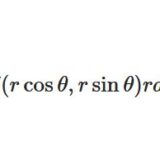
極座標変換による重積分の計算 ガウス積分を例に
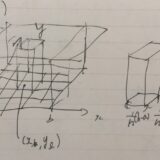
重積分とは? 逐次積分による計算法(フビニの定理)
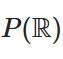
関数空間が無限次元とは? 多項式関数を例に

連続関数、可積分関数の線形空間(関数空間)、微分と積分の線形性とは
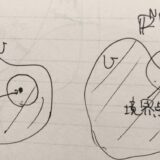
ユークリッド空間の開集合、閉集合、開球、近傍とは何か?
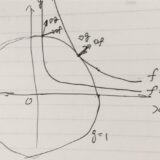
条件付き極値問題:ラグランジュの未定乗数法とは

