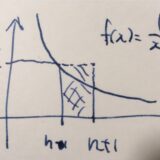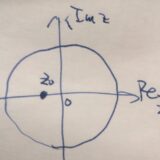
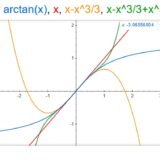
逆三角関数arctanのテイラー展開の簡単な求め方
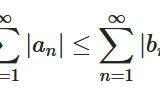
級数に関する不等式、比較判定法とは、その証明

収束する数列は有界であることの証明と応用
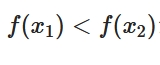
狭義単調増加(減少)関数が逆関数を持つことの証明
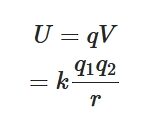
クーロン力による位置エネルギーを微積分によって導出
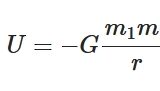
万有引力の位置エネルギーを微積分で導出・証明
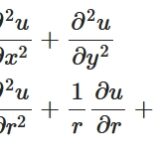
チェインルール:2次元極座標でのラプラシアンを例に
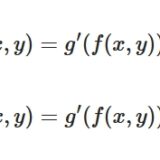
合成関数の偏微分、チェインルールとは:波動方程式を例に
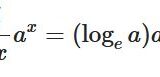
指数関数の微分の公式の覚え方、導出:指数関数の定義
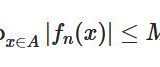
関数項級数の一様収束、Mテストとは:熱方程式への応用

指数関数の線形独立性とヴァンデルモンドの行列式の求め方
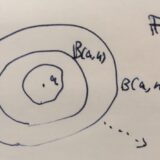
集合列の極限の求め方、例、上極限と下極限
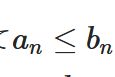
数列・関数の不等式が極限を取って保たれることについて

数列・関数の極限の性質:線形性、四則演算との交換

全微分とは:定義、十分条件と求め方、全微分可能でない例

方向微分、法線微分の定義、例、求め方

閉集合、触点、閉包、集積点、孤立点とは:定義、性質、例
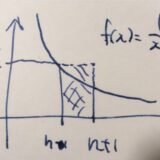
負のべき乗の無限級数Σ1/n^pの収束・発散の判定方法