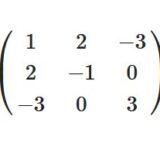
直交多項式とは:ルジャンドル多項式、微分方程式を例に
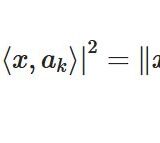
ベッセルの不等式・パーセバルの等式とは:有限のケースで証明
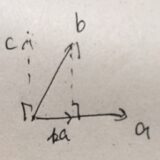
コーシー・シュワルツの不等式とは:証明と幾何学的な意味
三角関数の直交性とは:フーリエ級数展開と関数空間の内積
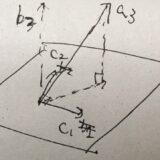
シュミットの直交化法とは:正規直交基底の具体的な求め方
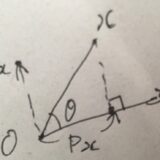
射影行列、射影作用素とは:例、定義、性質
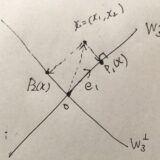
直交補空間、直交直和、直交射影とは:定義と例、証明
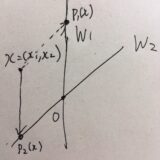
部分空間の直和とは:定義と例、射影

線形写像の単射・全射の条件:核・像、基底・次元との関係、証明
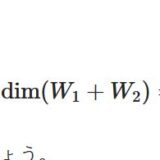
共通部分、和空間の次元の等式とは、その証明
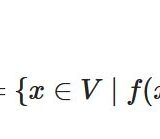
線形写像の核、像の定義:部分空間となることの証明
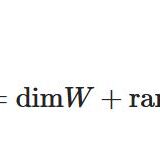
線形方程式の解空間とは:基底・基本解、次元の求め方
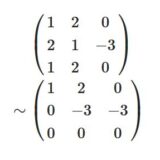
部分空間の基底、次元の求め方(生成、共通部分、和空間)
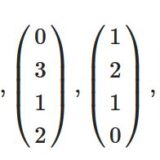
線形独立・従属の判定法:行列のランクとの関係

部分空間の共通部分、和空間とは:例と証明
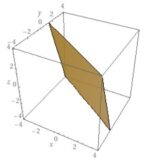
部分空間とは:例、判定法、証明の書き方
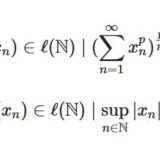
数列空間l^pとは、性質:ノルム、内積、無限次元
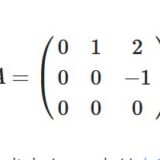
べきゼロ行列とは:例、指数行列、性質