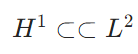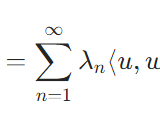
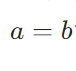
極限の一意性の証明:距離空間において
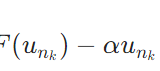
コンパクト対称作用素が作用素ノルムを固有値として持つことの証明
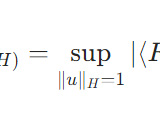
対称作用素の作用素ノルムの内積による表示の証明
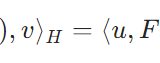
ヒルベルト空間の対称作用素とは:簡単な例
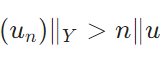
コンパクト作用素は有界作用素であることの証明
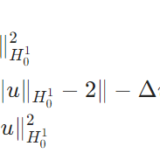
反応拡散方程式の力学系でアトラクターが存在することの証明
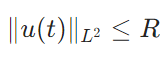
反応拡散方程式の力学系でL^2の吸収集合が存在することの証明
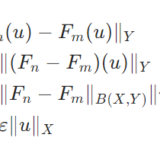
有界線形作用素のなす空間B(X,Y)がバナッハ空間となることの証明
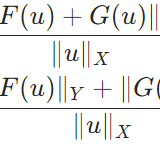
有界線形作用素のなす空間B(X,Y)がノルム空間となることの証明
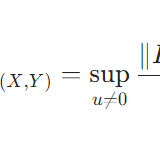
作用素ノルムの複数の定義が同値であることの証明

有界線形作用素のなす集合B(X,Y)が線形空間となることの証明
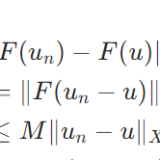
線形作用素の有界性と連続性は同値であることの証明
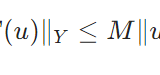
有界線形作用素、ノルムとは:行列、積分作用素、微分作用素の例
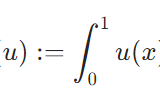
線形作用素・汎関数とは:行列、積分作用素、微分作用素の例

放物型偏微分方程式の弱形式、弱解とは
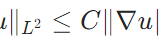
ポアンカレの不等式とは、証明、H_0^1ノルムへの応用
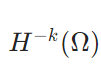
負の指数のソボレフ空間H^{-k}、双対空間とは
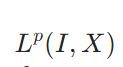
時間つき関数空間、バナッハ空間値関数とは