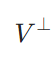
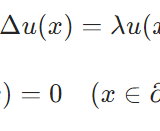
ラプラシアンが可算個の正の固有値を持つことの証明
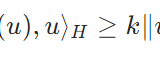
正値作用素とは:例、固有値が正となることの証明
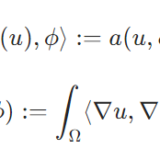
ラプラシアンが可逆であることの証明
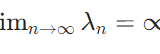
コンパクトな逆作用素を持つ作用素の固有値の性質
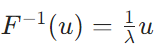
逆作用素の性質:線形性、固有値、対称性に関する証明
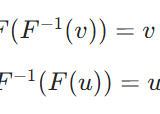
可逆作用素、逆作用素とは:定義、例を解説
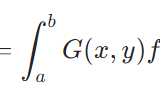
グリーン関数とは:常微分方程式の場合を簡単に
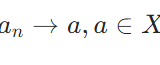
ノルム空間の有限次元部分空間が閉集合であることの証明
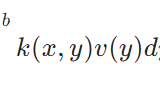
ストゥルム・リウビル型微分方程式の固有値の性質の証明
三角関数は多項式関数で表せないことの証明
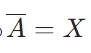
可分な空間とは、ヒルベルト空間において完全正規直交系の存在と同値であることの証明
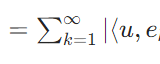
正規直交系の完全性とパーセバルの等式が同値であることの証明
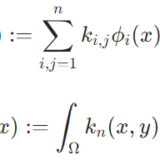
ヒルベルト・シュミット積分作用素がコンパクト作用素であることの証明
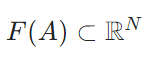
有限ランク作用素とは、コンパクト作用素であることの証明
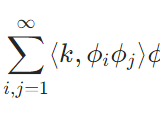
1変数の完全正規直交系から2変数の完全正規直交系が作れることの証明

コンパクト作用素が有界作用素のなす空間の閉部分空間であることの証明
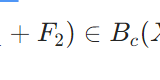
コンパクト作用素のなす集合が有界作用素のなす空間B(X,Y)の部分空間となることの証明
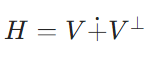
ヒルベルト空間の直交補空間による直和分解の証明