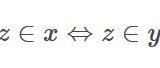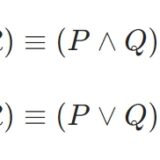
「集合論」の記事一覧
直線が「無限個の点の集まり」とは?
論理と集合の対応関係:ベン図を超えた理解へ
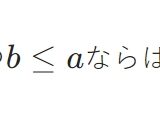
不等式の反対称律の証明:不等式の定義から
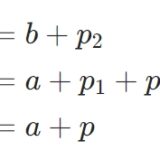
不等式の推移律の証明:定義に戻って考える、存在命題の練習
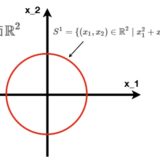
大学数学基礎:論理、証明、集合の記事まとめ
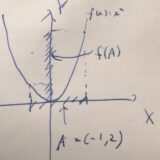
写像・関数の像の定義、例と求め方(一点集合、区間)
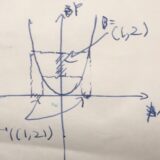
逆像の定義、例と求め方(一点集合、区間)
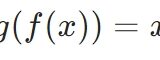
全単射と逆写像の存在が同値であることの証明、応用
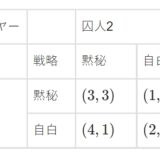
ゲーム理論入門:囚人のジレンマ、順序関係の応用(選好)
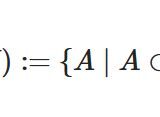
部分集合族(集合系)、べき集合とは何か:具体例と性質
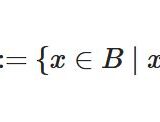
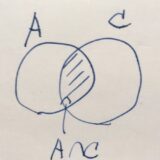
補集合、差集合、全体集合とは:例と性質、証明
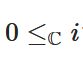
複素数で普通の順序・不等号・大小関係を考えないのはなぜか
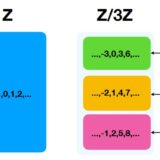
well-definedとは:代表元の取り方によらない確認はなぜ必要か
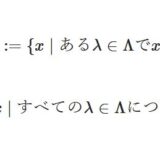
集合族の扱い方(和集合・共通部分):実数の区間を例に
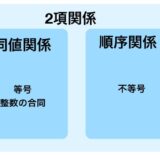
同値関係、2項関係とは? 整数の合同(mod)を例に
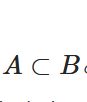
集合の要素、部分集合、等しいことの証明の書き方
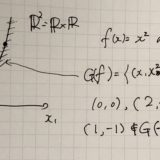
抽象ベクトル空間・線形空間の具体例R^N:順序対と直積集合

空集合が任意の集合の部分集合であるのはなぜか(空真)