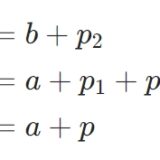不等式の反対称律の証明：不等式の定義から

どうも、木村（@kimu3_slime）です。

今回は、不等式の反対称律の証明について、定義にもとづいて紹介します。

未知の数\(x\)について、\(x \leq 5\)であり\( 5 \leq x\)のとき、\(x\)はどのような数でしょうか。それは\(x =5 \)以外にありえないですね。

一般に、すべての数\(a,b\)について、\(a \leq b\)かつ\(b \leq a\)ならば、\(a=b\)が成り立ちます。これは反対称律と呼ばれる不等式の性質です。

なぜ反対称律が成り立つのか、不等式・不等号の定義に遡って考えていきましょう。

一般に、数\(a,b\)について、\(a \leq b\)が成り立つとは、「\(a=b\)が成り立つか、または\( b = a+p\)を満たす正の数\(p\)が存在すること」と定義します。

0または正の数を非負の数と呼ぶことにすれば、\( b = a+p\)を満たす非負の数\(p\)が存在するとき、\(a \leq b\)と表すと言い換えられますね。

例えば、\(5 \leq 5\)が正しいのは、\(5=5\)が成り立つからです。一般に、すべての数\(a\)に対して\(a \leq a\)が成り立ち、その性質は反射律と呼ばれています。

この不等式の定義では、0、正の数、負の数が前提となっています。正の数とは何かについて議論することもできますが、今回はそれが目的でないので直観的に進みます。

では、反対称律（antisymmetric property）

すべての数\(a,b\)について、\(a \leq b\)かつ\(b \leq a\)ならば、\(a=b\)

を不等式の定義に戻って証明していきましょう。

仮定\(a \leq b\)から、\(b = a+p_1\)を満たす非負の数\(p_1\)が存在します。また、\(b\leq a\)から、\(a = b + p_2\)を満たす非負の数\(p_2\)が存在します。これらを組み合わせると、\(b= b+p_1+p_2\)となり、\(p_1 = – p_2\)が成り立ちます。

ここで\(p_1\)が正の数であることはありえません（背理法）。もし正の数だとすると、\(p_1 = -p_2\)から\(p_2\)が負の数となり、\(p_2\)が非負であることに矛盾します。よって、\(p_1\)は正の数でない非負の数、つまり0となります。したがって、\(p_2 =-p_1 =0\)です。以上により、\(a=b\)が成り立つことが示せました。

今回は等号を含む不等式\(\leq \)について反対称律を証明しましたが、等号を含まない不等式\(<\)でも成り立つ性質です。前提の\(a<b\)かつ\(b<a\)は成り立たないので（この条件を満たす数は存在しない）、「\(a \leq b\)かつ\(b \leq a\)ならば、\(a=b\)」は正しいと考えます（空真）。

等式\(=\)については、\(a=b\)ならば\(b=a\)が成り立ちます。これは対称律と呼ばれる性質です。

不等式では、対称律は成り立ちません。例えば、\(1 \leq 5\)は正しいですが、\(5 \leq 1 \)は正しくないからです。不等式が満たす一般的な性質は、反対称律となります。

以上、不等式の反対称律の証明について、定義にもとづいて紹介してきました。

反対称律は不等式の基本的な性質のひとつで、順序関係の公理のひとつでもあります。当たり前の性質ですが、不等式の定義から導けると論理が追えて良いですね。

木村すらいむ（@kimu3_slime）でした。ではでは。