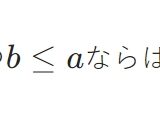どうも、木村(@kimu3_slime)です。
今回は、積のルートがルートの積となることの証明を紹介します。
数\(a,b\)が非負\(a\geq 0, b \geq 0\)のとき、
\[\sqrt{ab} = \sqrt{a} \sqrt{b}\]
が成り立ちます。
例えば、\(\sqrt{8} = \sqrt{2^2 \cdot 2 } = \sqrt{2^2}\sqrt{2} =2\sqrt{2}\)といったルートの計算でよく使われる性質ですね。
では、積のルートがルートの積となることを証明しましょう。
ルートの定義を確認すると、\(x \geq 0\)のとき、ルート\(\sqrt{x} \)は、二乗すると\(x\)になる正の数(正の平方根)のことでした。つまり、\(y^2 =x\)を満たす数\(y\)を\(y = \sqrt{x}\)と書くわけです。
この定義によれば、\(\sqrt{ab}= \sqrt{a}\sqrt{b}\)が成り立つことを示すには、右辺を二乗して\(ab\)になることを示せば良いです。計算してみると、実数の積は交換可能であることに注意して、
\[\begin{aligned} (\sqrt{a}\sqrt{b})^2 &= \sqrt{a}\sqrt{b}\sqrt{a}\sqrt{b}\\&= \sqrt{a} \sqrt{a}\sqrt{b}\sqrt{b} \\&= (\sqrt{a})^2 (\sqrt{b})^2 \\ &= ab\end{aligned}\]
となります。よって、\(\sqrt{ab}\)の定義から、\(\sqrt{ab}= \sqrt{a}\sqrt{b}\)が成り立つことが示せました。
この法則を分数の形で表せば、\(a \geq 0, b>0\)のとき
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]
が成り立つと言えます。\(b\)が分母なので、0で割るケースが定義されていないことに注意しましょう。
積のルートがルートの積に等しくなるためには、中身が非負の数である\(a\geq 0, b \geq 0\)という前提条件(\(\sqrt{a},\sqrt{b}\)が実数である)は必要です。
実際、\(a=-1,b=-1\)のとき、\(i = \sqrt{-1}\)は、虚数単位と呼ばれる複素数で、\(i^2 =-1\)を満たすように定義されています。
\[\sqrt{ab}= \sqrt{(-1)(-1)} = \sqrt{1} =1\]
\[\sqrt{-1}\sqrt{-1} = i^2 =-1\]
となり、\(\sqrt{ab} \neq \sqrt{a} \sqrt{b}\)が成り立ちます。複素数の場合は、ルートの積を簡単に扱えないことに注意しましょう。
今回は二乗根(ルート)について証明しましたが、\(n\)乗根でも同様です。
数\(a,b\)が非負\(a\geq 0, b \geq 0\)のとき、
\[\sqrt[n]{ab} = \sqrt[n]{a} \sqrt[n]{b}\]
が成り立ちます。
右辺を\(n\)乗すれば、
\[\begin{aligned} (\sqrt[n]{a}\sqrt[n]{b})^n &= \sqrt{a}\sqrt{b}\cdots \sqrt{a}\sqrt{b}\\&= (\sqrt[n]{a})^n (\sqrt[n]{b})^n \\ &= ab\end{aligned}\]
となるので。
\(n\)乗根だけでなく、無理数乗根、一般的なべき乗についても、\((ab)^p =a^p b^p\)が成り立ちます。
一般的なべき乗は、有理数乗で成り立っている等式\((ab)^{\frac{m}{n}} =a^{\frac{m}{n}} b^{\frac{m}{n}}\)が保たれるように、有理数乗の極限を使って定義されているので。詳しくは、杉浦「解析入門 Ⅰ」を参照してください。
以上、積のルートがルートの積となることの証明を紹介してきました。
僕が中学生だった頃は、\(\sqrt{ab} = \sqrt{a} \sqrt{b}\)という法則は当たり前だと思っていて、左辺と右辺の違いがよくわかっていませんでした。
しかし、これが当たり前の性質でないことは、複素数のケースを考えるとよくわかります。平方根とは何かの理解を試すのにちょうど良い問題だと思うので、ぜひ自力で証明できるようになってみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)
東京大学出版会 (1980-03-31T00:00:01Z)
¥1,799 (中古品)