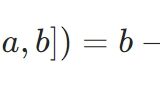どうも、木村(@kimu3_slime)です。
今回は、論理と集合の対応関係について、ベン図を超えた理解をする方法を紹介します。
| 論理 | 集合 |
| ならば \(\Rightarrow\) | 部分集合 \(\subset\) |
| かつ \(\land\) | 共通部分 \(\cap\) |
| または \(\lor\) | 和集合 \(\cup\) |
ならばの対応
\(P(x)\)を\(x\)は2の倍数である、\(Q(x)\)を\(x\)は4の倍数であるという文(変数を含む命題:述語)としましょう。
このとき、「もし\(x\)が4の倍数であるならば、\(x\)は2の倍数である」は必ず成り立ちますね。
これを「すべての\(x\)に対し、\(Q(x)\)ならば\(P(x)\)」が成り立つと呼びます。省略して、\(Q\)ならば\(P\)と言うこともあるでしょう。
参考:「すべての」「存在する」「一意性」とは? 証明の書き方
この論理の視点を、集合に移してみましょう。集合は、文によって定義できます(内包記法)。
\[A := \{x \mid P(x)\}\]
\[B := \{x \mid Q(x)\}\]
\(A\)は\(P(x)\)を満たす\(x\)の集合、つまり2の倍数の集合です。\(B\)は4の倍数の集合です。
例えば、\(4\)は\(A\)の要素ではありませんが、\(B\)の要素ではあります。このことを、\(4 \not\in A \)、\(4 \in B\)と表します。
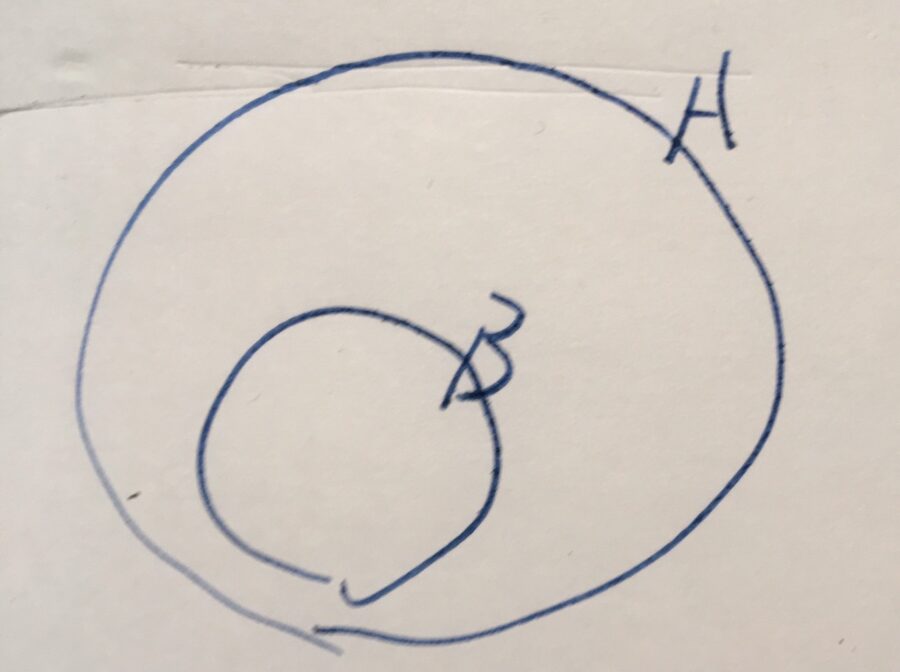
このとき、\(B\)の要素\(x\)はすべて\(A\)の要素でもありますね。これを\(B\)は\(A\)の部分集合であるといい、\(B \subset A\)と書きます。
つまり、「すべての\(x\)に対し、\(Q(x)\)ならば\(P(x)\)」という論理的な含意の関係は、\(B \subset A\)という集合的な包含関係として表されたわけです。
この状況をベン図を使って表せば、次のようになります。
かつ、またはの対応
もうひとつ、別の条件
\(R(x):x は 3の倍数である\)
とそれに対応する集合
\[C :=\{x \mid R(x)\}\]
を考えましょう。\(C\)は3の倍数の集合です。
「\(P\)ならば\(R\)」やその逆は成り立っていませんし、\(A \subset C\)やその逆も成り立っていません。
ただし、両者の共通部分や合わせた対象を考えることはできます。
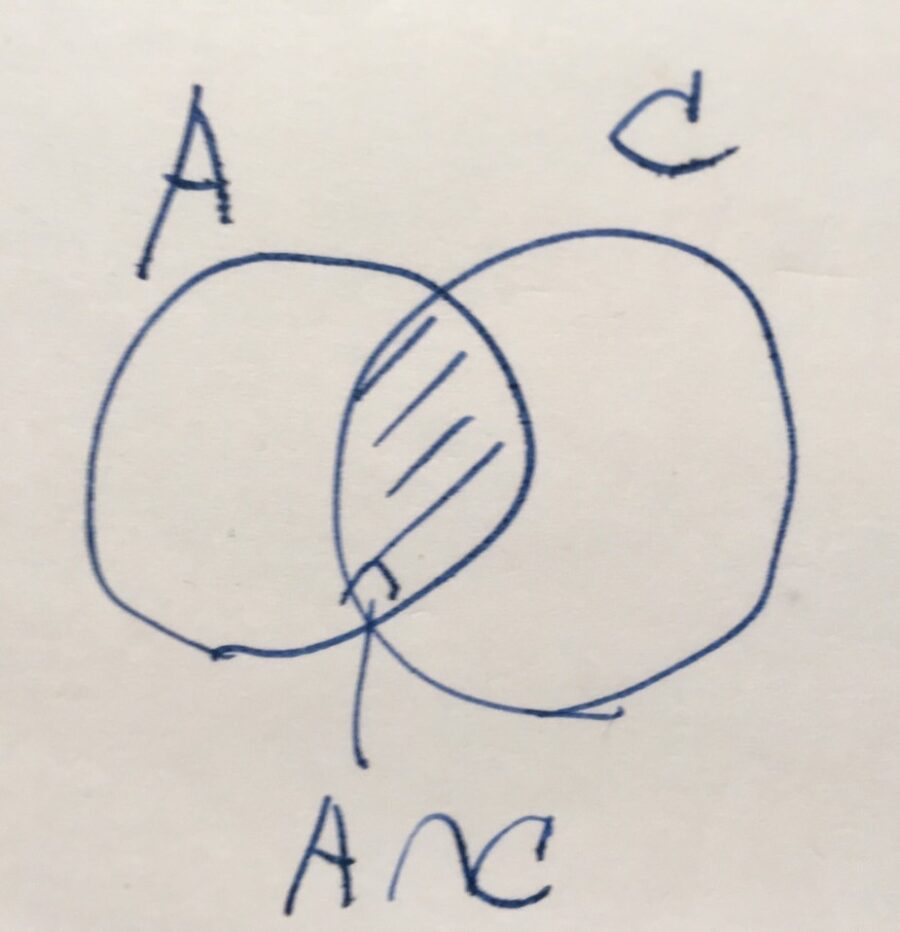
「\(P(x)\)かつ\(R(x)\)」という文を考えましょう。\(x\)は\(2\)の倍数であり、かつ\(3\)の倍数でもあるということです。これを集合の言葉を使えば、
\[\begin{aligned} A \cap C &:= \{ x \mid x \in A かつ x \in C\}\\ &= \{x \mid P(x) かつ R(x)\} \end{aligned}\]
と表せます。これを\(A\)と\(C\)の共通部分、積集合と呼びます。
例えば、\(4 \not \in A \cap C\)で、\(6 \in A\cap C\)です。
「\(P(x)\)かつ\(R(x)\)」という論理の言葉は、\(A \cap C\)という集合の言葉に対応しましたね。
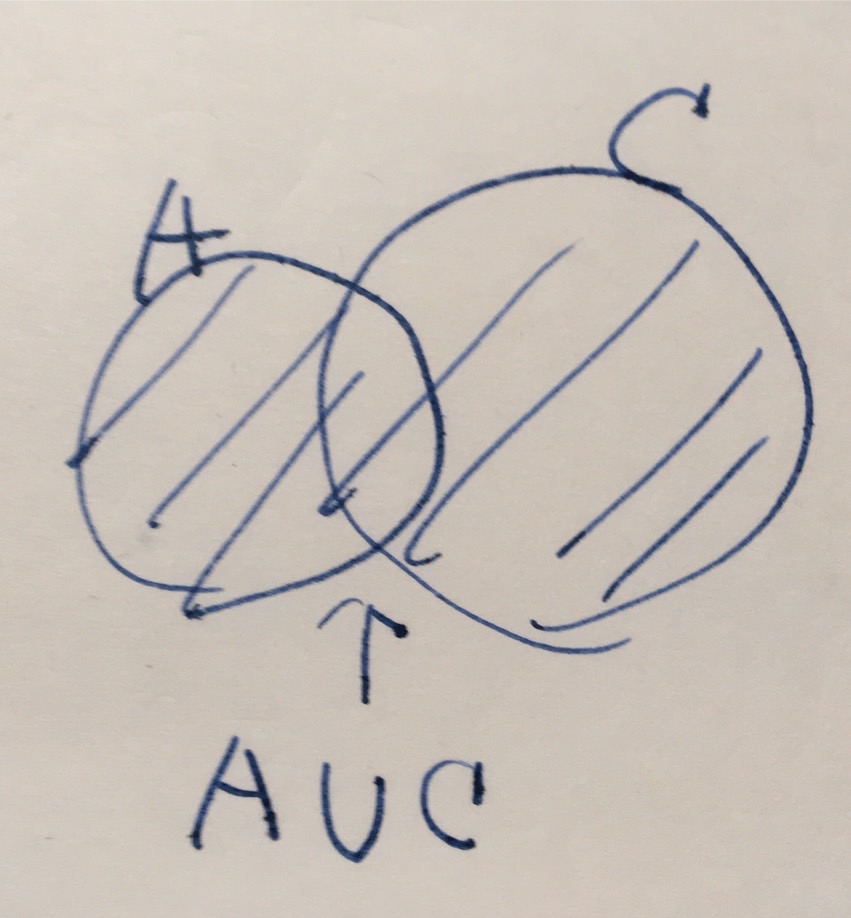
続いて、2つの条件のどちらか一方でも満たせば良いこと、「\(P(x)\)または\(R(x)\)」について考えましょう。集合の言葉を使えば、
\[\begin{aligned} A \cup C &:= \{ x \mid x \in A または x \in C\}\\ &= \{x \mid P(x) または R(x)\} \end{aligned}\]
と表せます。これを\(A\)と\(C\)の和集合と呼びます。
例えば、\(4 \in A \cup C\)で、\(5 \not \in A\cup C\)です。
「\(P(x)\)または\(R(x)\)」という論理の言葉は、\(A \cup C\)という集合の言葉に対応しましたね。
| 論理 | 集合 |
| ならば \(\Rightarrow\) | 部分集合 \(\subset\) |
| かつ \(\land\) | 共通部分 \(\cap\) |
| または \(\lor\) | 和集合 \(\cup\) |
以上、論理と集合の対応関係について紹介してきました。
高校数学の論理と集合の分野では、しばしばそれらの関係がベン図によって説明されるのを目にします。
ベン図は視覚的な扱いとしてはわかりやすいですが、それしか扱わないと、論理と集合の関係がはっきりとしません。
論理の言葉を集合の言葉でまとめて表現できることから、集合論は数学の基礎として大学で学ばれています。
論理と集合の対応関係を理解した上で、ベン図はそれらを視覚的に表現する補助的な手段として活用できると良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
日本評論社 (2008-12-01T00:00:01Z)
¥2,860
Richard Hammack (2019-07-19T00:00:01Z)
¥3,378