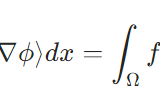
「微分方程式論」の記事一覧
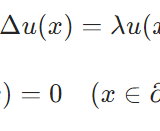
ラプラシアンが可算個の正の固有値を持つことの証明
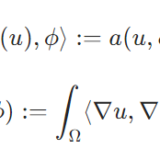
ラプラシアンが可逆であることの証明
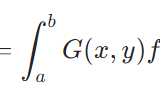
グリーン関数とは:常微分方程式の場合を簡単に
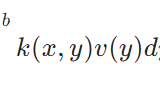
ストゥルム・リウビル型微分方程式の固有値の性質の証明
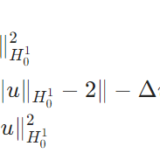
反応拡散方程式の力学系でアトラクターが存在することの証明
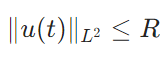
反応拡散方程式の力学系でL^2の吸収集合が存在することの証明

放物型偏微分方程式の弱形式、弱解とは
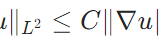
ポアンカレの不等式とは、証明、H_0^1ノルムへの応用
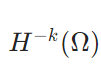
負の指数のソボレフ空間H^{-k}、双対空間とは
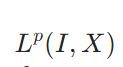
時間つき関数空間、バナッハ空間値関数とは
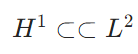
レリッヒ・コンドラショフの定理、コンパクト作用素、コンパクトな埋込みとは
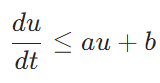
グロンウォールの不等式とは、証明
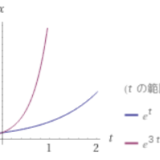
常微分方程式の比較定理とは、証明

ローレンツ方程式のアトラクターの存在証明
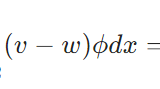
弱微分の一意性の証明:変分法の基本補題を利用して

グローバルアトラクターとは:散逸系における存在、例
一点と集合の距離、集合間の距離とは:ユークリッド空間を例に
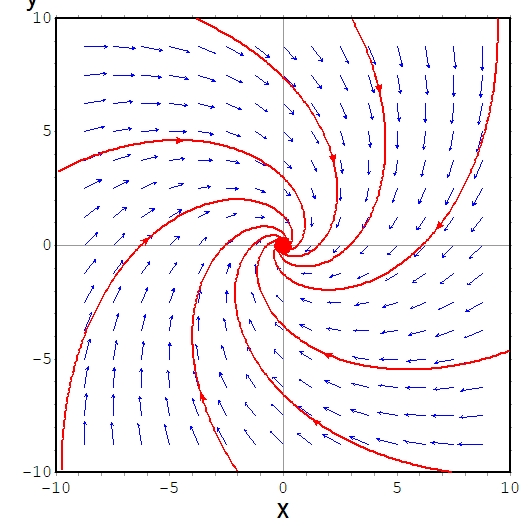
吸収集合、散逸系とは:線形力学系を例に