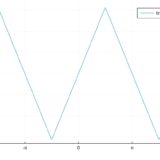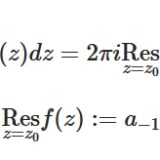
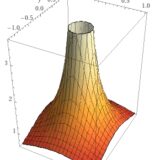
ローラン展開とは:求め方、孤立特異点の分類(極、除去可能特異点、真性特異点)
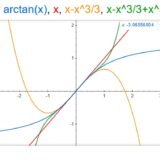
逆三角関数arctanのテイラー展開の簡単な求め方

収束する数列は有界であることの証明と応用
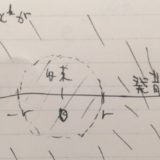
べき級数の収束発散が円盤によって分かれること:収束半径の性質
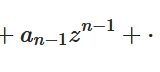
代数学の基本定理とは:リウビルの定理による証明
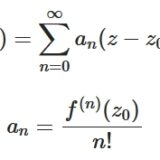
複素関数のテイラー展開(べき級数展開)とは、証明
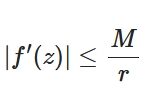
複素解析におけるリウビルの定理とは:例と証明
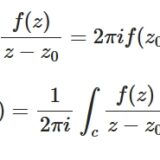
コーシーの積分公式とは、計算例と応用(無限回微分可能、コーシーの不等式)
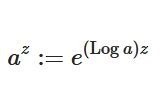
複素数の複素数乗、べき乗・指数関数の主値とは何か、計算例
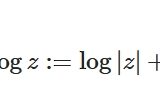
複素対数関数の主値Log zとは、計算例
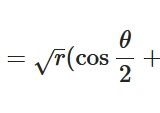
複素関数の主値、多価関数・一価関数とは:平方根、ルートを例に
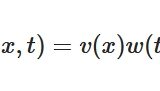
偏微分方程式が変数分離法によって解けるのはなぜか
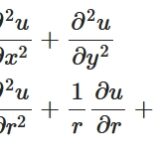
チェインルール:2次元極座標でのラプラシアンを例に
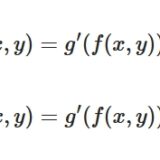
合成関数の偏微分、チェインルールとは:波動方程式を例に
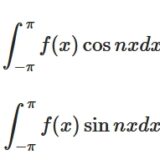
フーリエ係数の減衰:リーマン・ルベーグの補題とは、証明
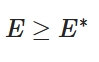
フーリエ係数の最良性とは:証明、ベッセルの不等式、パーセバルの等式
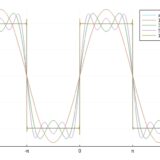
フーリエ級数の収束条件:L^2収束、一様収束、不連続点での値
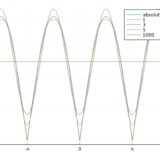
絶対サイン波|sin x|とは:フーリエ級数展開の求め方