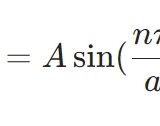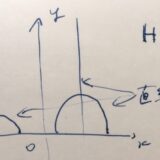
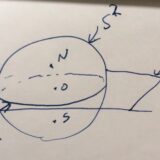
球面の幾何学入門:平行な直線が存在しないこと
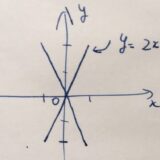
図形の線対称・点対称とは:行列変換の立場から
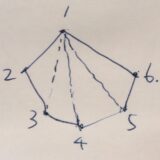
多角形の対角線の本数の求め方:n(n-3)/2となることの証明
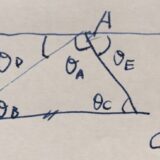
三角形の内角の和が180度であることの証明:補助線、平行線公準を用いて
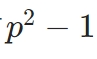
5以上の素数pについてp^2-1が24の倍数となることの証明
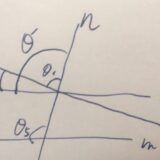
平行線の性質の逆「同位角・錯角が等しい直線は平行」の証明
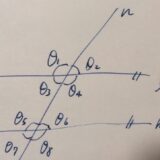
同位角・錯角とは:平行線の錯角の大きさが等しいことの証明
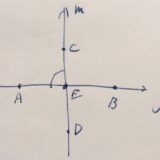
垂直な直線の定義、直角に交わることの証明
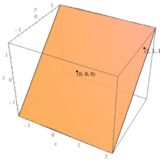
公準「平面上の異なる2点を含む直線は平面内にあること」の線形代数による説明
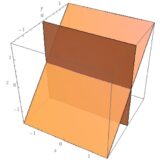
交わる平面の共通部分が直線であること:線形代数による説明
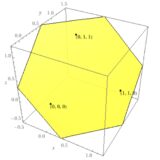
公準「共線的でない3点に1つの平面が定まる」とは:基底による説明
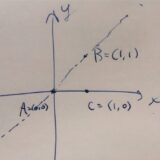
1点、2点、3点を通る直線の個数について:座標を用いて証明

数学における良い定義の4条件とは:線分を例に
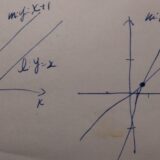
傾きが等しい直線は交わらない(平行)ことの証明、平行の定義
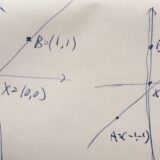
3つの点が共線的とは:線形独立性との関係
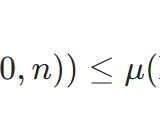
直線の長さが無限とは:ルベーグ測度による説明
直線が「無限個の点の集まり」とは?
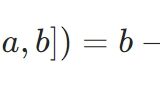
点に大きさがないとは:ルベーグ測度による説明