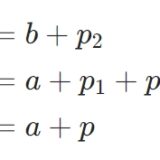1次元自由粒子の波動関数：境界条件から三角関数となるのはなぜか

どうも、木村（@kimu3_slime）です。

1次元の空間を自由に運動している粒子（例えば電子）を考え、その波動関数を\(\Psi(x)\)としましょう。それはシュレーディンガーの波動方程式

\[ – \frac{h^2}{8\pi^2 m_e} \frac{d^2 \Psi (x)}{dx^2} =E \Psi(x)\]

を満たすことが知られています。特に1次元の箱における運動、つまり区間\(0 \leq x \leq a\)、\(a>0\)という区間を考え、

\[\Psi(0) =\Psi(a)=0\]

という境界条件（ディリクレ境界条件）を考えましょう。このとき、境界条件から波動関数は

\[\Psi(x) = A \sin (\frac{n\pi}{a} x)\]

と三角関数で表されると教科書などで説明されますが、これがなぜなのか紹介していきましょう。

まず、

\[ – \frac{h^2}{8\pi^2 m_e} \frac{d^2 \Psi (x)}{dx^2} =E \Psi(x)\]

という形の方程式は、未知の関数\(\Phi\)に関する微分方程式です。特に、同次形の2階線形常微分方程式に分類されます。

この方程式は解き方が知られていて、\(\lambda\)を方程式の係数により決まる定数として、解は次のいずれかになります。

\[ \begin{aligned} \Psi(x) = \left\{ \begin{array}{l} C_1 e^{\sqrt{\lambda} x} + C_2 e^{\sqrt{-\lambda}x} & \lambda>0 \\ C_1 + C_2 x & \lambda =0 \\ C_1 \cos{\sqrt{-\lambda}x } + C_2 \sin {\sqrt{-\lambda}x } & \lambda <0 \end{array} \right. \end{aligned} \]

これが第3のケース、三角関数に限られることを、境界条件\(\Psi(0)=\Psi(a)=0\)を使って確かめてみましょう。

\(\Psi(0)=\Psi(a)=0\)なので、

\[ \begin{aligned} \left\{ \begin{array}{l} C_1+C_2 = C_1 e^{\sqrt{\lambda}a} + C_2 e^{-\sqrt{\lambda}a} =0 & \lambda>0 \\ C_1 = C_1+C_2 a =0 & \lambda =0 \\ C_1 = C_1 \cos(\sqrt{-\lambda} a) + C_2 \sin (\sqrt{-\lambda} a) =0 & \lambda <0 \end{array} \right. \end{aligned} \]

\(\lambda>0\)のとき。\(C_1= -C_2\)なので、\( C_1 e^{\sqrt{\lambda}a} -C_1 e^{-\sqrt{\lambda}a}=0\)で、\( C_1 e^{ 2\sqrt{\lambda}a} =C_1\)。\(e^{ 2\sqrt{\lambda}a} >1\)なので、\(C_1=0\)です。

\(\lambda =0\)のとき。\(C_1 =0\)より、\(C_2 a =0\)で、\(a\neq 0\)なので\(C_2 =0\)です。

つまり、\(\lambda\geq 0\)のとき、\(C_1 = C_2=0\)となって自明解\(\Psi(x) \equiv 0\)しか見つかりません。これは波動関数の規格化条件\(\int_{0}^a |\Psi(x)| ^2 dx =1\)（粒子がどこかに存在すること）に反するので、このケースは話が進みません。

\(\lambda<0\)のときを考えましょう。

\(C_2 \neq 0\)で、かつ\(C_2 \sin (\sqrt {-\lambda}a) =0\)となる\(\lambda\)を求めると、

\[\sqrt {-\lambda}a = n \pi \]

\[ \begin{aligned}\lambda = – \frac{n^2 \pi ^2}{a^2} ,\quad n \in \mathbb{N}\end{aligned} \]

したがって、\(\Psi(x)= C_2 \sin (\frac{n\pi}{a} x)\)となることが導けました。これが三角関数が導かれる理由です。

以上、1次元自由粒子の波動関数について、境界条件から三角関数となるのはなぜかを紹介してきました。

この議論は、1次元の熱方程式の解を境界条件から絞り込むのと同じ議論です。常微分方程式の境界値問題で三角関数が表れる話はよくあるので、理屈まで込みで理解できると良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。