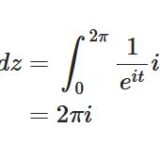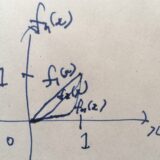
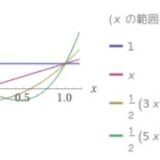
直交多項式とは:ルジャンドル多項式、微分方程式を例に
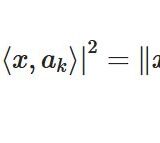
ベッセルの不等式・パーセバルの等式とは:有限のケースで証明
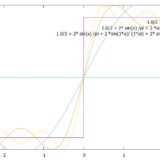
三角関数の直交性とは:フーリエ級数展開と関数空間の内積

有理数と分数、無理数の違い:よくある誤解を越えて
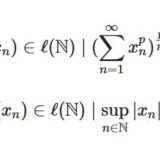
数列空間l^pとは、性質:ノルム、内積、無限次元
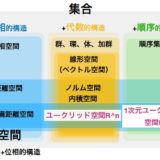
環、体とは何か:数、多項式、行列、Z/nZを例に
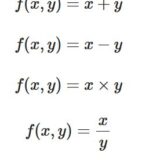
数学における演算とは:二項演算、単項演算の簡単な例

高校数学から始める公理的確率論:標本空間、事象、確率とは

確率の定義「場合の数」とは何か:結果の個数である
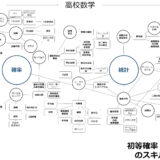
初等確率・統計のスキルツリー:必要な中学・高校数学
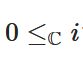
複素数で普通の順序・不等号・大小関係を考えないのはなぜか
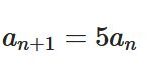
漸化式と微分方程式は似ている:簡単な例で解説
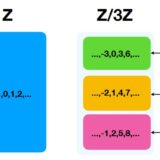
well-definedとは:代表元の取り方によらない確認はなぜ必要か
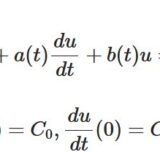
線形微分方程式はなぜ指数関数e^{λt}と仮定して解いて良いか

微分方程式の解でなぜ指数関数(exp・ネイピア数)が現れるか
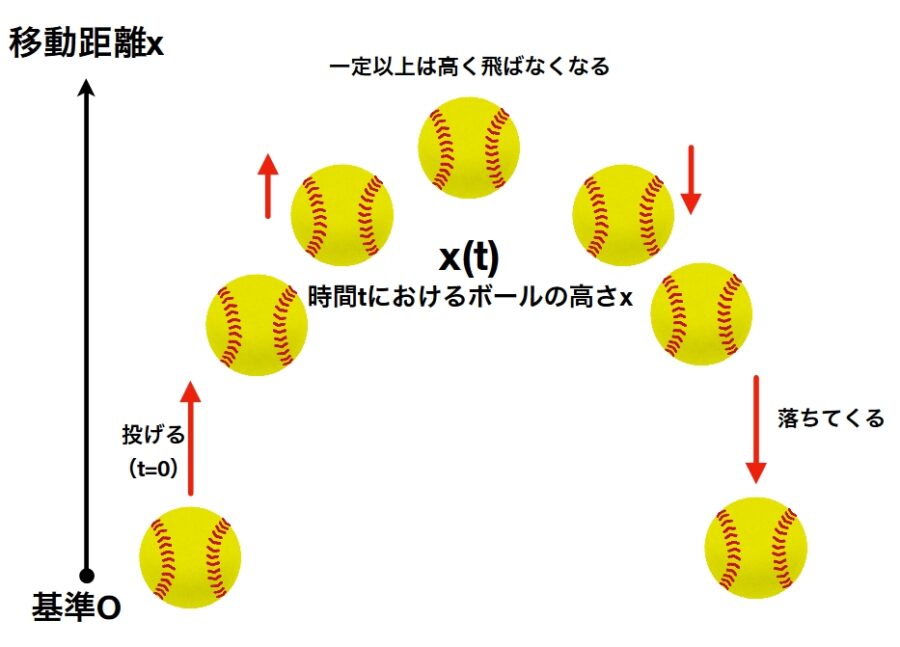
不定積分と定積分をなぜ学ぶか 微分方程式の一般解と特殊解
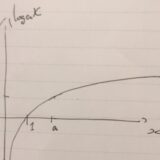
対数logの外し方、外せる条件と対数関数の性質
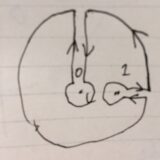
コーシーの積分定理とは:積分路の変形、証明