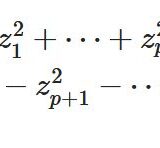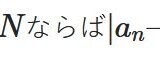
積分の絶対値に関する三角不等式とは:例と証明
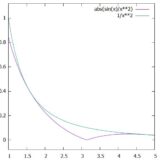
広義積分の絶対収束の比較判定法:ガンマ関数を例に
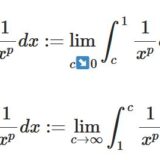
負のべき乗の広義積分の収束・発散条件
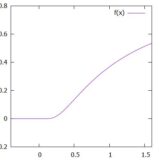
無限回微分可能であるがテイラー展開できない例について
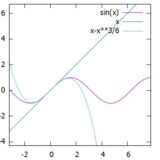
三角・指数・対数関数と多項式の不等式:テイラー展開に関連して
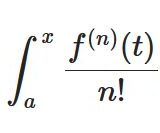
テイラーの定理の積分を用いた導出:積分形の剰余項
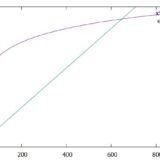
多項式・指数・対数関数の極限、増大のスピード比較
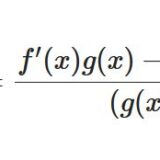
商f/gの微分公式の覚え方:合成関数・積の微分による導出・証明

有名な極限の公式f(x)/xの覚え方:接線近似とテイラー展開
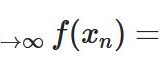
関数の連続(極限)と数列連続(点列連続)の定義が同値であることの証明
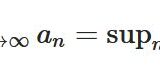
数列と上限・下限の関係:有界な単調数列は収束する
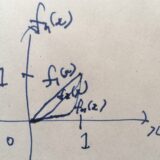
関数列の各点収束、一様収束とは、例と違い、求め方
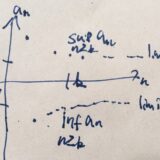
数列の上極限・下極限(limsup,liminf)の例、性質
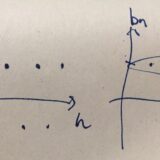
部分列、ボルツァーノ・ワイエルシュトラスの定理とは:点列コンパクトとの関係
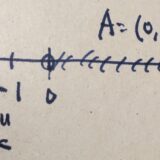
上限・下限(sup,inf)、有界とは:具体例、最大・最小値との違い
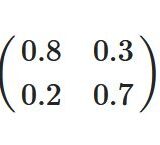
非負行列・正行列のペロン・フロベニウスの定理とは、証明
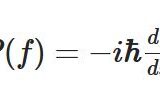
なぜ複素の線形代数を考えるか:運動量演算子のエルミート性
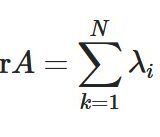
行列のトレースをなぜ学ぶか:不変量と応用