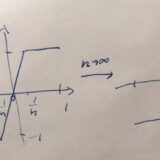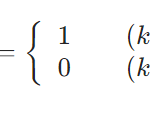
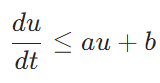
グロンウォールの不等式とは、証明
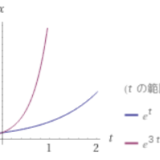
常微分方程式の比較定理とは、証明
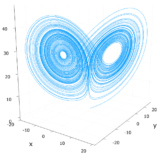
ローレンツ方程式のアトラクターの存在証明
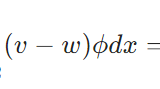
弱微分の一意性の証明:変分法の基本補題を利用して

グローバルアトラクターとは:散逸系における存在、例
一点と集合の距離、集合間の距離とは:ユークリッド空間を例に
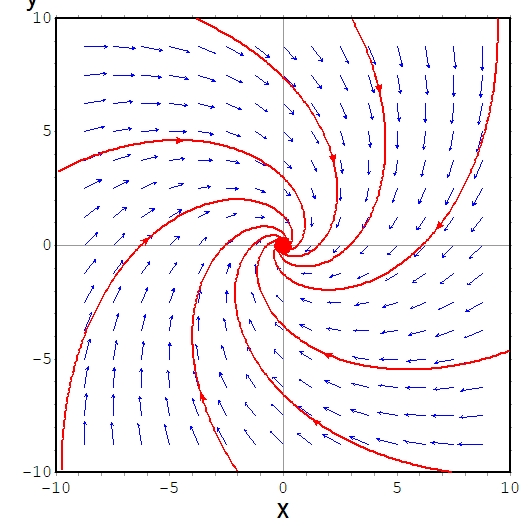
吸収集合、散逸系とは:線形力学系を例に
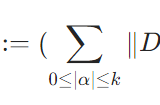
ソボレフ空間W^{k,p}・H^kが線形、ノルム、内積空間となることの証明
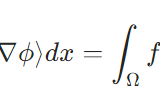
弱形式、弱解とは:ポアソン方程式を例に
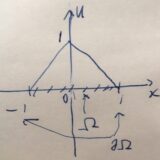
境界で0のソボレフ空間W_0^{k,p},H_0^kとは
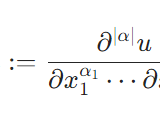
ソボレフ空間W^{k,p},H^kとは:多重指数、ノルム、内積
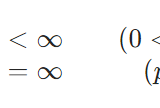
p乗可積分な関数とは:負のべき乗、L^1だがL^2でない例
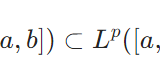
有界閉区間上の連続関数はp乗可積分であることの証明
ほとんど至る所(a.e.)とは:簡単な関数を例に
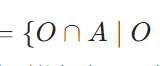
相対位相、部分集合における開集合・閉集合とは:ユークリッド空間の位相を例に
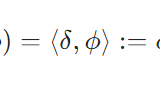
超関数、超関数微分とは:ディラックのデルタ関数を例に
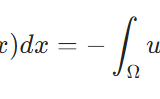
弱微分、ソボレフ空間W^{k,p},H^kとは:簡単な例
テスト関数C_c^∞、関数の台とは:簡単な例