「力学系理論」の記事一覧

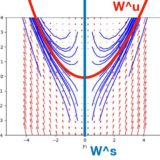
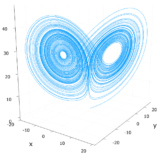
ローレンツ方程式のアトラクターの存在証明

グローバルアトラクターとは:散逸系における存在、例
一点と集合の距離、集合間の距離とは:ユークリッド空間を例に
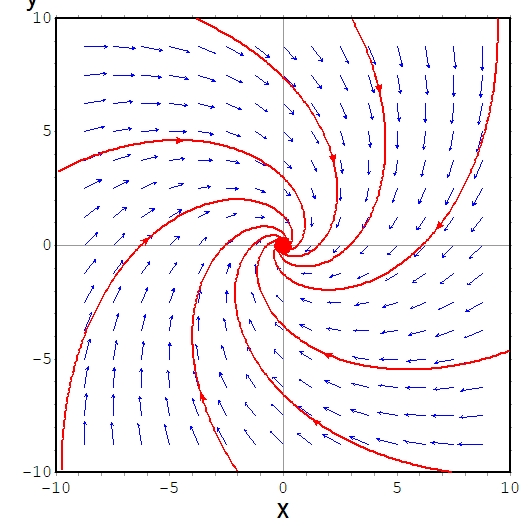
吸収集合、散逸系とは:線形力学系を例に
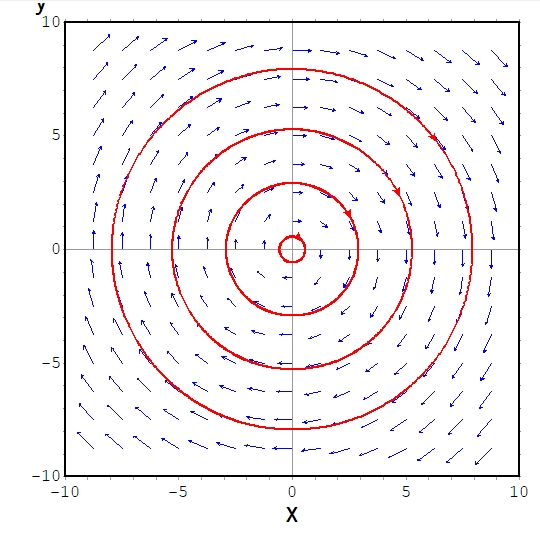
解作用素、抽象力学系とは:偏微分方程式の力学系入門
ファンデルポール方程式、リミットサイクルとは
非線形バネの方程式とは:平衡解の安定性を調べる
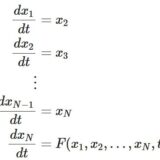
高階常微分方程式の連立形への書き換えについて
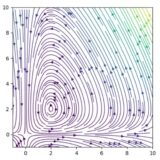
ロトカ・ヴォルテラ方程式の平衡解の安定性、解曲線の求め方
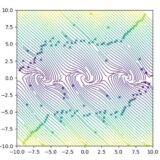
減衰振り子の力学系:平衡解の安定性を線形化して調べる
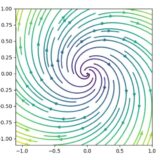
2次元線形力学系の平衡解の分類:スパイラル(渦状点)とは
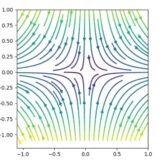
2次元線形力学系の平衡解の分類:サドル(鞍点)とは
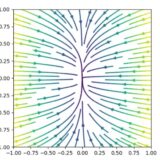
2次元線形力学系の平衡解の分類:ノード(結節点)とは
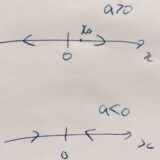
1次元の線形力学系とは:相図の書き方、安定性
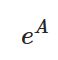
線形常微分方程式を行列で解く:行列の指数関数を解説
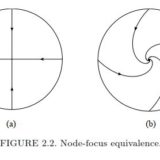
力学系の構造安定性について簡単に紹介
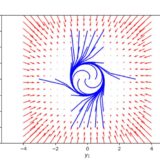
極限集合の性質を明らかにするポアンカレ・ベンディクソンの定理
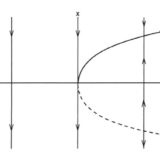
力学系の分岐理論、分岐図を簡単な例で解説