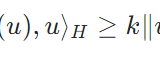どうも、木村(@kimu3_slime)です。
今回は、ラプラシアンが可算個の正の固有値を持つことの証明を紹介します。
導入
\(\Omega \subset \mathbb{R}^N\)を有界な領域とし、
\[-\Delta u(x) = \lambda u(x)\]
\[u(x) = 0 \quad(x \in \partial \Omega)\]
を満たす\(\lambda\)と関数\(u\)を、(ディリクレ)ラプラシアンの固有値、固有関数と呼びます。どんな固有値や固有関数を持つのでしょうか。
1次元の場合は簡単でイメージしやすいでしょう(参考:1次元ラプラシアンの固有値問題の解き方、固有関数とは)
より具体的に、弱形式のラプラシアン\(A=-\Delta\)を考えましょう。\(A:H_0^1(\Omega)\to H^{-1}(\Omega)\)は、\(\phi \in H_0 ^1 (\Omega)\)に対し、
\[\langle A(u),\phi \rangle := a(u,\phi)\]
\[a(u,\phi):=\int_\Omega \langle \nabla u, \nabla \phi \rangle dx \]
と定義されています。
このラプラシアンの固有値は、次のような性質を持ちます。
- 固有値はすべて実数で、正であり、可算無限個。
- \(\lambda_{n} \leq \lambda_{n+1}\)となるように番号付けするとき、\(\lim_{n\to \infty}\lambda _n = \infty\)
- 固有関数系\((w_n)\)は、\(H_0^1(\Omega)\)の要素であり、\(L^2(\Omega)\)の完全正規直交系となる。
特に、最小の固有値\(\lambda_1>0\)をラプラシアンの主固有値(principal eigenvalue)と呼びます。
証明
ヒルベルト・シュミットの定理から導かれる、コンパクトな逆作用素を持つ対称作用素の性質に持ち込みましょう。
対称性
固有値が実数となることを示すために、\(A\)が対称作用素であることを示しましょう。
内積の対称性から、
\[\begin{aligned} &\langle A(u),v\rangle \\ &= a(u,v)\\&=\int_\Omega \langle \nabla u, \nabla v \rangle dx \\&= \int_\Omega \langle \nabla v, \nabla u \rangle dx\\&=a(v,u)\\ &=\langle A(v),u\rangle \end{aligned}\]
となるので、対称作用素です。
コンパクトな逆作用素を持つこと
ラプラシアンが\(H_0^{-1}\)を余定義域として逆作用素を持つことは別の記事にて示しました。
特に、\(A^{-1}(f)=u\)となるとき、\(\|u\|_{H_0^1}= \|f\|_{H^{-1}}\)となっています。
関数からは有界線形汎関数が定まるので、\(L^2(\Omega)\subset H_0^{-1}(\Omega)\)とみなせます。したがって、\(A:L^2(\Omega) \to L^2(\Omega)\)と見て、\(A\)は全射です。
\(A^{-1}:L^2(\Omega) \to L^2(\Omega)\)がコンパクト作用素であることを示しましょう。
\(u \in L^2\)を\(H^{-1}\)として見る、すなわち\(\langle T_u ,v\rangle := \langle u,v\rangle_{L^2}\)として定まる線形汎関数\(T_u\)について考えましょう。コーシー・シュワルツの不等式とポアンカレの不等式\(\|v\|_{L^2}\leq C \|\nabla v\|_{L^2}=C\|v\|_{H_0^1}\)から
\[\begin{aligned} & |\langle T_u ,v\rangle|\\ &\leq \|u\|_{L^2}\|v\|_{L^2} \\&= C\|u\|_{L^2}\|v\|_{H_0^1} \end{aligned}\]
となるので、作用素ノルムの定義から\(\|T_u\|_{H^{-1}}\leq C\|u\|_{L^2}\)です。
したがって、\(f \in L^2\)として、\(A^{-1}\)は有界作用素なので(有界逆作用素定理)、
\[\begin{aligned} &\|A^{-1}(f)\|_{H_0^1} \\ &=\|u\|_{H_0^1}\\&= \|T_u\|_{H^{-1}} \\&\leq C\|u\|_{L^2} \\&= C\|A^{-1}(f)\|_{L^2} \\& \leq C\|A^{-1}\|_{B(L^2,L^2)}\|f\|_{L^2} \end{aligned}\]
となります。これは\(L^2\)の有界集合の\(A^{-1}\)による像は\(H_0^1\)において有界であることを意味します。ポアンカレの不等式より、\(H_0^1\)で有界であることと\(H^1\)で有界であることは同値です。そして、レリッヒ・コンドラショフの定理より\(H^1\)の有界集合は\(L^2\)においてコンパクトです。
したがって、\(L^2\)における有界集合を\(B\)とすると、\(A^{-1}(B)\)は\(H_0^1\)において有界で、さらに\(L^2\)においてコンパクトになります。よって、\(A^{-1}\)がコンパクト作用素であることが示せました。
固有値が正であること
ラプラシアンが正値作用素であり、固有値がすべて正となることは別記事にて示しました。
ヒルベルト・シュミットの定理の適用
以上により、コンパクトな逆作用素を持つ作用素の固有値の性質が使えます。
\(H\)を可分なヒルベルト空間とし、その部分空間\(D(G)\)を定義域とする線形作用素\(G:D(G)\to H\)を考えます。さらに、\(G\)は対称で、全射\(R(G)=H\)で、可逆な作用素であり、逆作用素\(G^{-1}\)はコンパクトとします。
このとき、
- 固有値はすべて実数
- (\(H\)が無限次元であるとき)固有値は可算無限個。
- すべての固有値が正であるとき、すべての\(n \in \mathbb{N}\)に対し\(|\lambda_{n+1}| \geq |\lambda_{n}|\)」を満たすように固有値に番号付けするならば、\(\lim_{n \to \infty} \lambda_n =\infty\)
- 固有関数系\((w_n)\)は、\(H\)の完全正規直交系(ヒルベルト基底)となる。
- \(G(u) = \sum_{n=1}^\infty \lambda_{n}\langle u,w_n\rangle w_n\)と表せる。
となります。
\(H=L^2(\Omega)\)で、\(G=A\)、\(D(A)=H_0^1(\Omega)\)としています。\(A\)は対称で全射\(R(A)=H\)で、可逆であり、逆作用素はコンパクトなので、前提を満たしています。また、固有値はすべて正であることも示しました。また\(L^2\)は無限次元です。
よって、
- 固有値はすべて実数で、正であり、可算無限個。
- \(\lambda_{n} \leq \lambda_{n+1}\)となるように番号付けするとき、\(\lim_{n\to \infty}\lambda _n = \infty\)
- 固有関数系\((w_n)\)は、\(H_0^1(\Omega)\)の要素であり、\(L^2(\Omega)\)の完全正規直交系となる。
となることが示せました。
関連する結果
証明はしませんが、これに関連する結果を紹介しておきましょう。
- 固有関数系は\(H_0^1(\Omega)\)の要素であるだけでなく、\(C^\infty(\Omega)\)となります(レギュラリティの議論)。つまり固有関数は強い意味(古典的な意味)で微分可能で、(強い意味での)ラプラシアンの固有関数が見つけられています。
- 主固有値\(\lambda_1\)は単純です。つまり、固有空間が1次元、固有関数は定数倍の違いしかありえません。
- 主固有値の変分原理:主固有値はレイリー商\(\lambda_1=\min_{u\in H_0^1, u \neq 0} \frac{\langle A(u),u\rangle}{\|u\|_{L^2}}\) で表せる。
- ここまでの議論はラプラシアンに限らず、それを一般化した楕円形作用素\(L\)について成り立つ。
以上、ラプラシアンが可算個の正の固有値を持つことの証明を紹介してきました。
符号はこちらでは\(-\Delta\)を考えているので反転していますが、今回の結果はそれを一般化するものです。多次元の領域においてもラプラシアンには可算個の固有値があり、固有関数が\(L^2\)の完全正規直交系というのは非常に強力な結果ですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)
こちらもおすすめ
無限集合の濃度とは? 写像の全単射、可算無限、カントールの対角線論法