「微分方程式論」の記事一覧
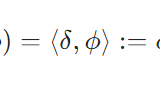
超関数、超関数微分とは:ディラックのデルタ関数を例に
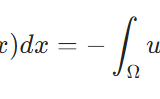
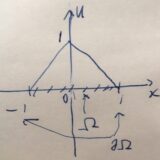
弱微分、ソボレフ空間W^{k,p},H^kとは:簡単な例
テスト関数C_c^∞、関数の台とは:簡単な例
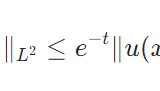
熱方程式のエネルギー評価とは:単純な例
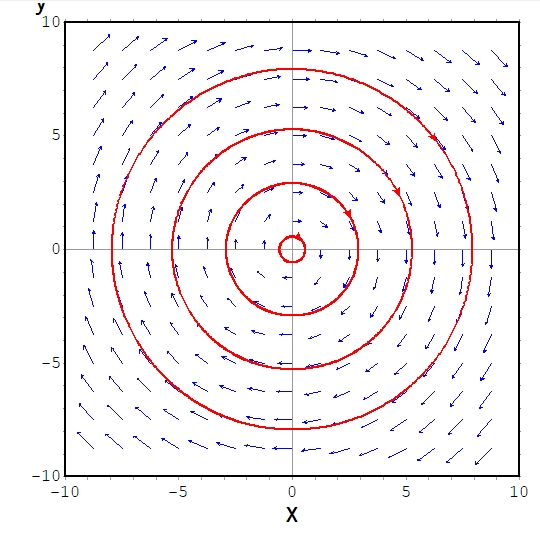
解作用素、抽象力学系とは:偏微分方程式の力学系入門
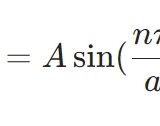
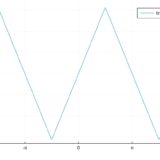
1次元自由粒子の波動関数:境界条件から三角関数となるのはなぜか

雪だるま式な増加とは:微分方程式、指数関数による表し方

微積分の応用:1次反応の半減期、放射性炭素年代測定法とは
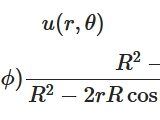
複素解析におけるポアソンの積分公式とは、ポアソン核との関連
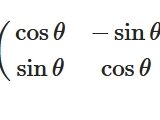
ラプラシアンが回転不変であること:2次元での証明
円環領域におけるポテンシャル:2次元ラプラス方程式の解き方
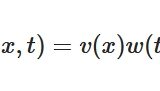
偏微分方程式が変数分離法によって解けるのはなぜか
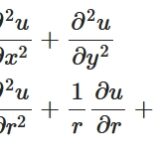
チェインルール:2次元極座標でのラプラシアンを例に
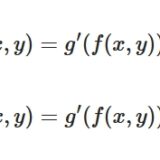
合成関数の偏微分、チェインルールとは:波動方程式を例に
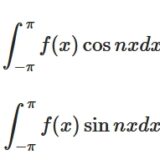
フーリエ係数の減衰:リーマン・ルベーグの補題とは、証明
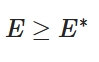
フーリエ係数の最良性とは:証明、ベッセルの不等式、パーセバルの等式
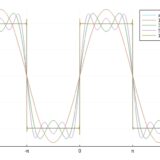
フーリエ級数の収束条件:L^2収束、一様収束、不連続点での値
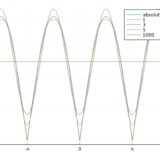
絶対サイン波|sin x|とは:フーリエ級数展開の求め方