どうも、木村(@kimu3_slime)です。
「借金が雪だるま式に増える」など、小さな変化の積み重ねがやがて大きな結果をもたらすことの表現として、雪だるま式という表現があります。英語ではsnowball effect(雪玉効果)です。
今回はそれを数学的に、微分方程式、指数関数によって表してみましょう。

半径\(r\)の雪玉を転がすことを考えましょう。雪の地面を動かし、位置\(x\)での雪玉の半径を\(r(x)\)(位置の関数)とします。
雪玉を動かすとき、半径の拡大率は微分\(\frac{dr}{dx}\)で表せます。これは何に等しいと考えれば良いでしょうか?
雪玉を動かすとき、そこにくっつく雪は自転車の車輪のように一次元的であると考えましょう。すると、くっつく雪は、雪玉という球の一部分、横から平面的に見れば円周の長さに比例します。雪玉の円周は、\(2\pi r\)と半径\(r\)に比例します。
地面に接する円周の割合、地面から雪玉にくっつく雪の割合などを含めて、増加率は\(a r\)であるとしましょう。ただし、\(a>0\)です。これらをまとめれば、
\[\frac{dr(x)}{dx} = a r(x)\]
という関数の微分を含む方程式、微分方程式ができあがりました。
この方程式は簡単に解くことができて、
\[ r(x) = r(0) e^{ax}\]
という指数関数が解です(微分すれば確かめられます)。
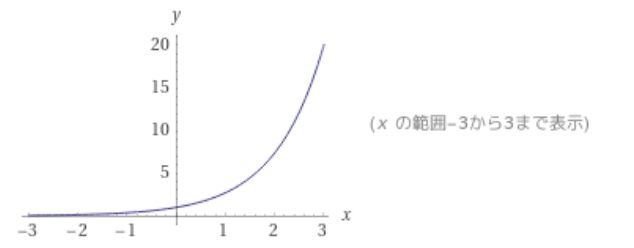
この関数は1次関数や2次関数よりも速く増加し、文字通り雪だるま式に増加する状況が表せています。
\(a=0.001\)で、最初の雪玉の大きさが\(r(0)=1\) cmだったとしましょう。\(x = 3000\) cm、つまり30m動かしたとき、このモデルに従う雪玉はどこまで大きくなるでしょうか。
\(r(3000) = 1 e^{0.001 \times 3000}\)をコンピュータを使って計算すると、約20cmと求めることができました。
非現実的な話ですが、\(x= 10000\)とすると、約22000cmまで大きくなります。現実には雪玉自体が重くて動かせなくなるのと、動かすスペースや地面の雪が足りなくなるわけですが。
以上、雪だるま式な増加とは何か、微分方程式、指数関数による表し方を紹介してきました。
「変化率は半径に比例する」という微分方程式からは、加速度的に増加する指数関数が得られます。慣用表現ですが、それを数学的に考えてみるのも面白いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1978-03-23T00:00:01Z)
¥3,900 (中古品)